Null Convention Logic Signals II

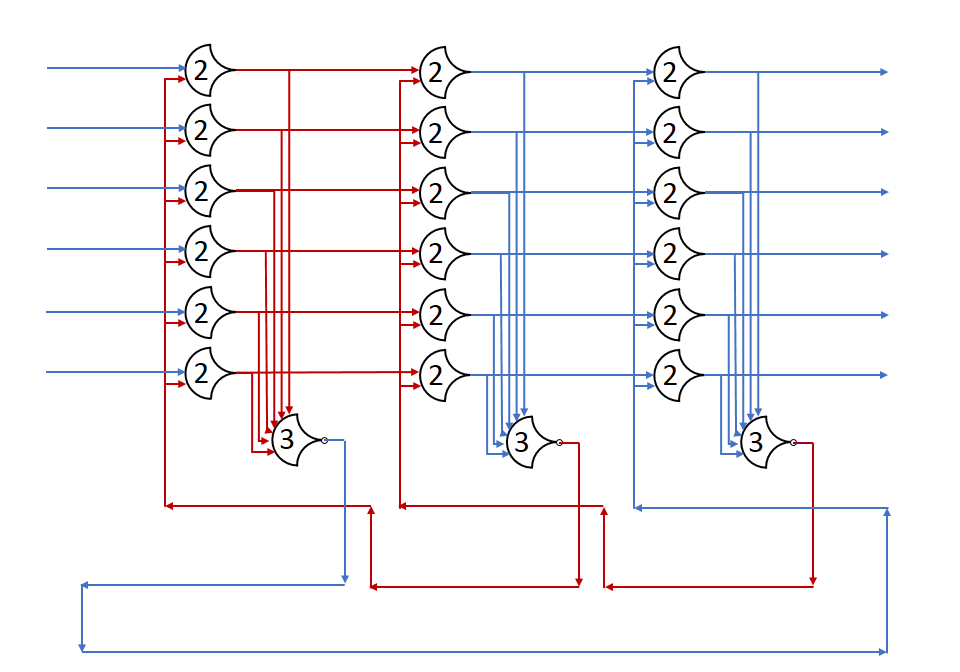
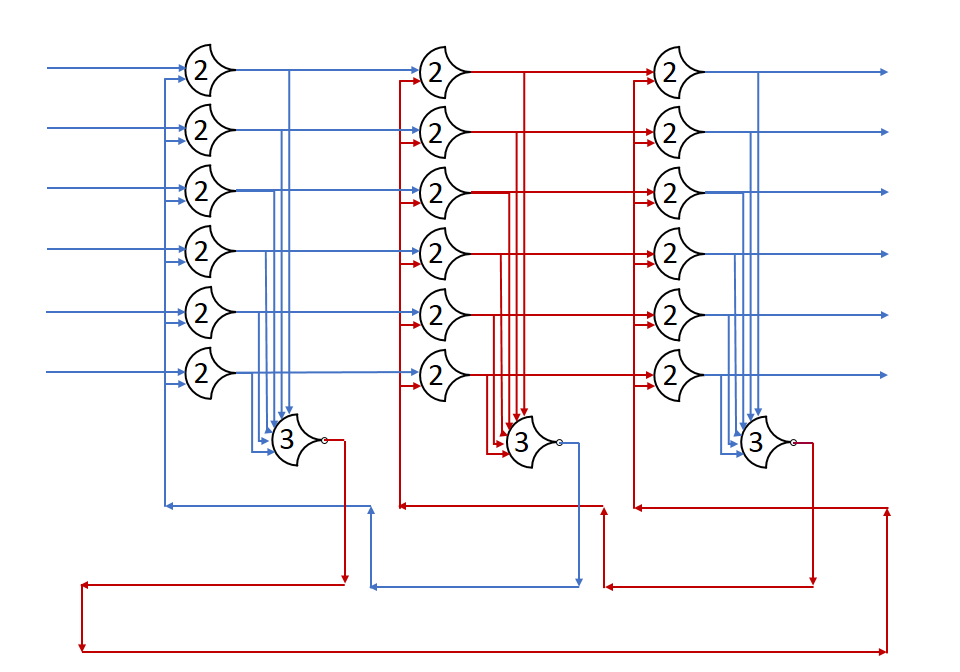
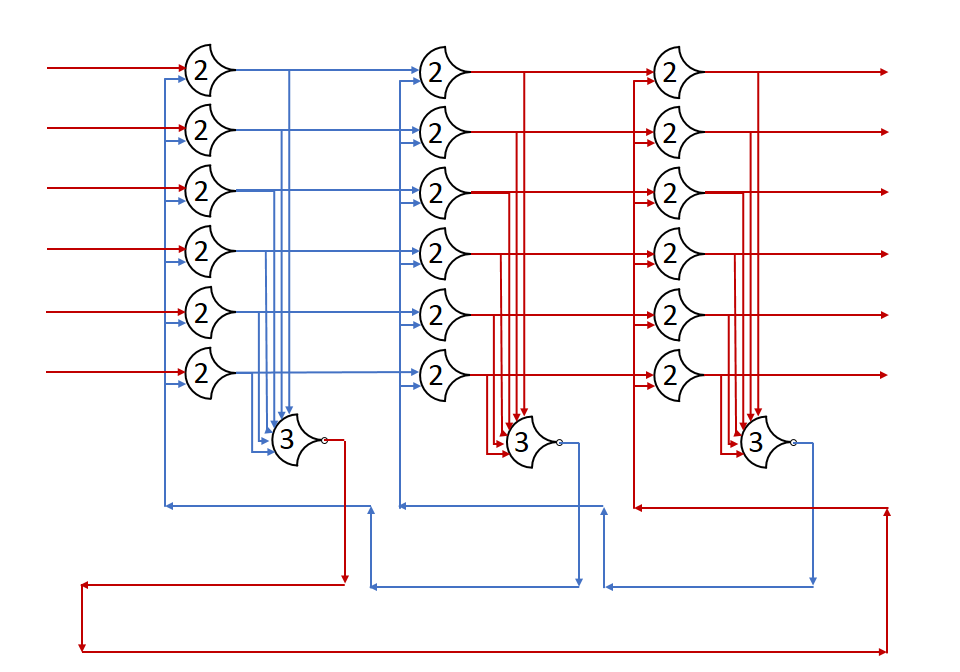
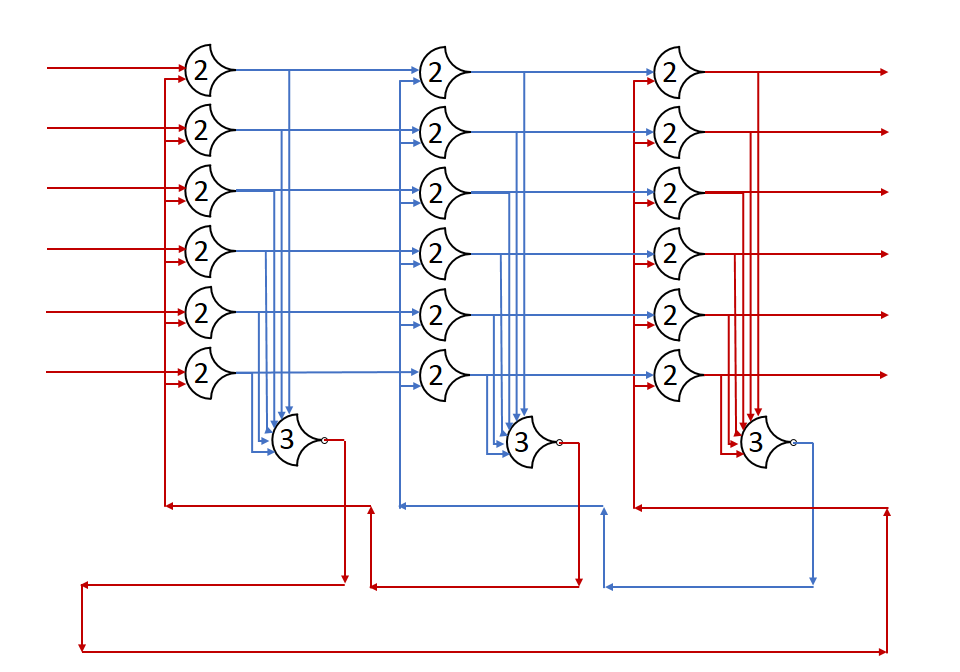
Background

My naming conventions have probably been misleading. I have mostly treated NCL bits as three-state logic (NULL, DATA0, and DATA1) this is a valid way to work with the data, but it is limiting. The better way to think of it is as individual 2-state logic lines (NULL and DATA).

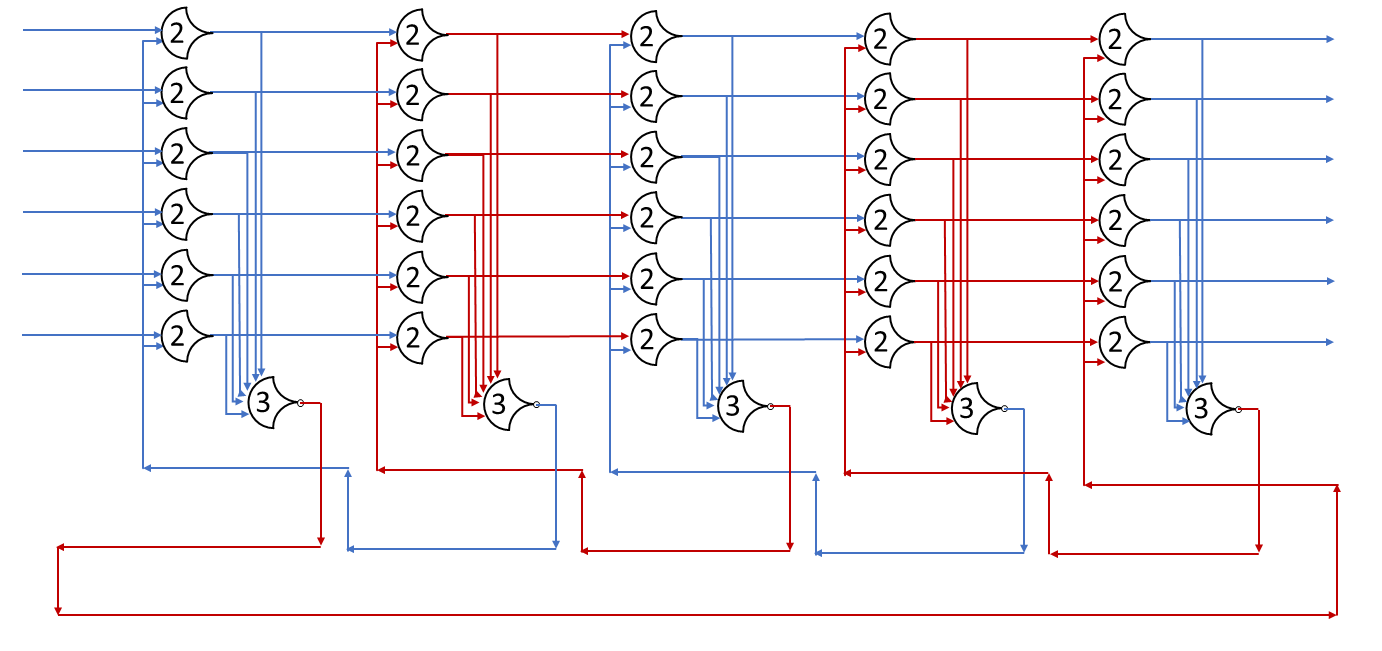
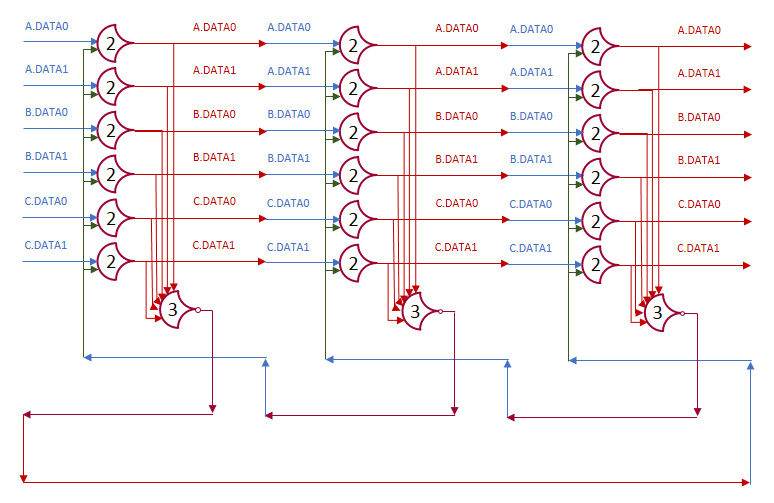
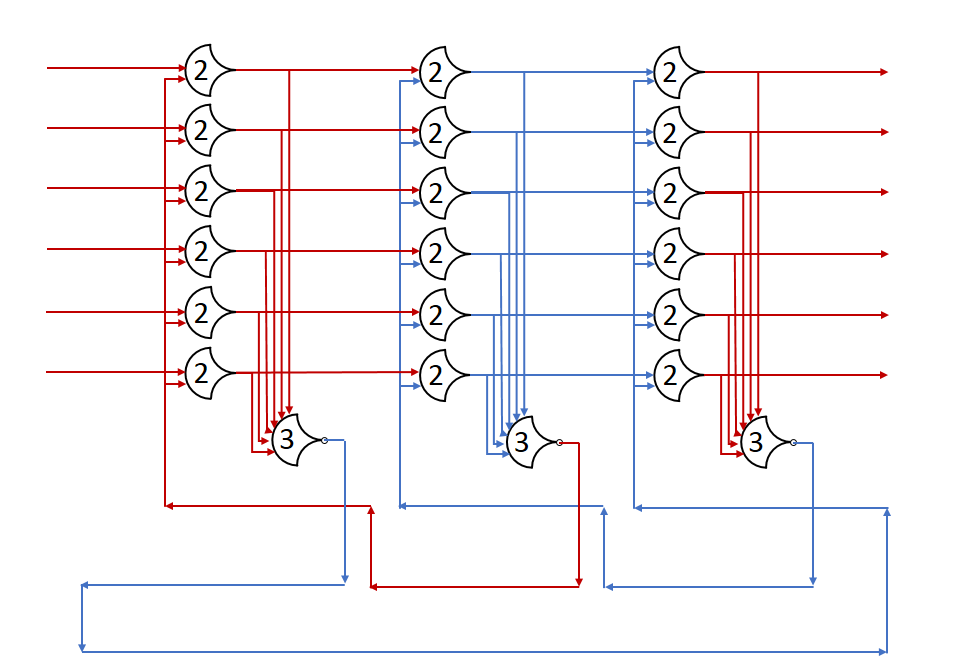
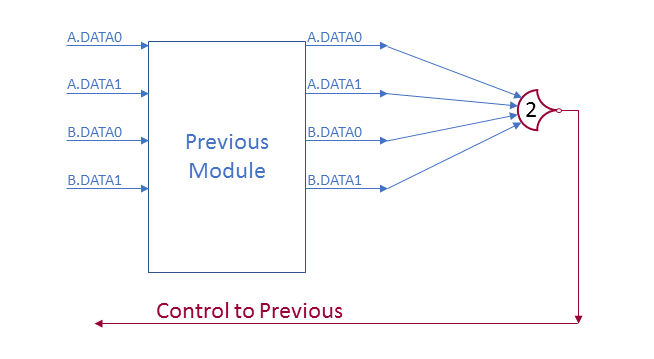
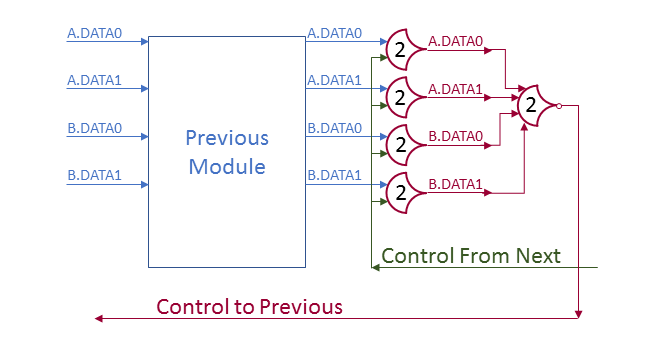
Internally to a component, using single-rail signals is very helpful. Not only are single-rail signals the inputs to all NCL gates, but they can be used as links between components as well. Single-rail signals cannot really be passed through registers because they have to be asserted for the DATA wave to read as complete. This would prevent the signal from conveying meaning, as it would always have the same value during computations.

My Theory

This section is unverified theory. Please share your thoughts below.

I will b using _ to refer to a non-asserted rail (null) and ^ to refer to an asserted rail (data).

Another benefit of this view is that you get more flexibility in state encodings. Standard encodings (that I’ve come across) use mutually exclusive data lines. So a 3-rail signal would have 3 possible states and a 4-rail signal would have 4 states. By thinking of the data more in terms of DATA and NULL, you get to design your own state encodings. For example, with a 4-rail encoding, you could use the following 6 states: {__^^, _^_^, _^^_, ^__^, ^_^_, ^^__}.

State Space Restrictions

A state space is the set of valid states. We will use it here a little more specifically to refer to the valid DATA states. Not all state spaces will actually work for NCL, The completion logic has to be able to correctly identify completed states. For example, if we try to use the following for a 3-rail signal, we have a problem: {__^, _^^, ^^^}. If the result is the last state (^^^) and the data on line 0 arrives first, the completion logic will see it as a complete __^ and pass on the wrong result.

For any state, it has to be able to partially arrive, without looking like another state. This is required for delay insensitivity. A simple way to make this happen is to use M-hot states. By that I mean that each state will have the same number of rails asserted as data (^), and all such states can be used. The number of states in such an assignment for a N-rail signal is M Choose N or C(M, N). This has its maximum value when M=N/2. It also has the benefit that any incomplete state has at most M-1 rails set, which will never match another state.

The logic proof-y version: ∀x,y∈S:(x&y!=x) and (x&y!=y) must hold (& is the bitwise AND operator) where S is the state space.

Using this N/2-hot encoding, the states/rail is

Rails	States	State Increase Factor
1	1
2	2	2
3	3	1.5
4	6	2
5	10	1.6667
6	20	2

Using this encoding, you get nearly twice as many states for each rail you add. Using mutually-exclusive rails (1-hot) you get 1 extra state per rail. Even if you break it up into 2-rail pairs and use combinations of those values, you only double your state space for every 2 rails you add. In the table above, s you increase the number of rails, the factor approaches 2 for the odd numbers of rails as well.

In special cases, you might want a more complex encoding, some examples of valid state spaces:

{___^, ^_^_, _^__}
{__^^, ^___, _^__}
{^^^_, ^^_^, ^_^^, _^^^}
{^^^_, ___^}
{__^^, _^_^, _^^_, ^__^, ^_^_, ^^__}

Takeaway

While you can increase the compatibility of your modules by using a standard state space, sometimes you can reduce the number of rails by using more dense encodings. Additionally, signals that exist only between registers (are not passed on) can actually be 1-rail signals, which is something I have a hard time remembering when integrating components. These 1-rail signals can act as enable signals: They can be used to prevent data from propagating, or to allow it to propagate (remember steering).

August 2, 2017

Steering

Problem

In Null Convention Logic, all computation is done with oscillating DATA/NULL cycles. The NULL cycles clear the whole circuit, the DATA cycles perform the computation. This requires 2 transition sets per computation (Previous DATA => NULL => Next DATA). Sometimes the DATA output from a component will not be used (think the unselected inputs of a MUX).

Solution

When using steering, the DATA wavefront is only passed to the necessary components. In the case of a MUX, the outputs of these components are then combined as needed with TH1n gates:

Steering

The TH22 gates in this example do not allow the DATA wavefront to apss into the components unless they are selected by the DMUX1. During any particular DATA wavefront, only one of these components will be active at a time; the other component will remain NULL. This saves transitions, and thus power. This method also works if only some, or no inputs are shared.

Details

The DMUX1 component is a decoder, that only outputs the DATA1 lines. Technically, I think it matches the NCL network criteria, if you consider the outputs to be single rail outputs, which have only one DATA value. The DMUX1 is used to enable only the selected component.

We will use steering when our ALU has more than just the Adder with glue logic. At some point we’ll have a multiplier, and a shifter, only one of these will operate at a time.

For more on steering, see Karl Fant’s site. His blog posts have lots of good theory too.

July 31, 2017

Register Ring with Multiple Wavefronts

In this post, we built a ring of registers and set a data wavefront loose in it. We added many stages, and watched the single wavefront run through them. In this post, I’ll show what happens with multiple wavefronts.

Theory

First, we should establish how many registers we need for some number of wavefronts. From the Register Ring post, we know that in order for a state (DATA or NULL) to pass on, the next two stages must both be in the opposite state. This prevents the passage from overwriting the next stage’s state completely, as it has already passed on to the next stage.

Here, the DATA state (red) can move on to the next stage because the NULL state has been passed up to the 3rd stage. By overwriting the 2nd stage, no state is lost, because stage 2 has already finished with the NULL state.

Here, stage 2 cannot pass DATA on to stage 3 because that would remove the NULL state entirely. If there were 4 stages, and the 4th was NULL, then the 3rd stage could accept data, since the NULL state would be preserved.

As you can see, the number of stages in a state is not important, but rather the sequence must be preserved. Let’s assume a really long line of registers for a moment, with stage states: (DATA, NULL, NULL, DATA, ...) All of these NULLs can be assumed to be the same logical state, which we’ll refer to as NULL1, we’ll also call the first DATA state DATA1: (DATA1, NULL1, NULL1, DATA0, ...). Take the case where the last DATA wave can’t move because of some really slow stage after it. If we ‘run’ the system for a register delay, the DATA1 state progresses, and overwrites one of the NULL1 states, but there are still some left, so nothing is really lost. When DATA1 moves forward, a NULL state fills its stage; this is a new state, so let’s call it NULL2: (NULL2, DATA1, NULL1, DATA0, ...). If we run again, one might expect the DATA1 state to advance again, but taht would overwrite the NULL1 state completely, putting two distinct DATA states right next to each other. Having two adjacent DATA states prevents the components from resetting between them, which only produces correct results if the DATA states are identical. Since there is no guarantee that DATA1 and DATA0 are identical, we have to preserve the NULL between them.

There are states which would be deadlocked, however, as long as the initial conditions are valid (not deadlocked), the handshaking ensures that these states never occur as a propagation of the circuit.

Some examples:

Ring: (NULL, DATA, NULL, DATA) (4 states) – Nothing can pass, the system is deadlocked (we can’t actually get here naturally)
Ring: (NULL, DATA, NULL, NULL) (2 states) – Only the DATA state can pass, the NULLs are contiguous, so they can be considered to be identical states
Ring: (NULL, DATA, DATA, NULL) (2 states) – Both states can pass, the DATA can overwrite the NULL in position 4, and the NULL can overwrite the DATA in position 2
Ring: (NULL, DATA, DATA, DATA) (2 states) – Only NULL can pass, if DATA was able to pass, the NULL could be deleted from the system
Ring: (NULL, NULL, DATA, NULL) (2 states) – Only DATA can pass, if NULL was able to pass, the DATA could be deleted from the system
Rotations of these work out to the same thing since it’s a ring

Note that DATA and NULL are symmetric and the values in the DATA wave don’t matter. You can swap instances of ‘NULL’ and ‘DATA’ and get a valid result.

In short, with an even number of stages, you can only have N/2 states. What about odd numbers?

Ring: (NULL, DATA, NULL, NULL, DATA) (4 states) – Only the first DATA can move, as it is the only stage followed by 2 of the opposite state
Ring: (NULL, DATA, DATA, NULL, DATA) (4 states) – Only the first NULL can move, as it is the only stage followed by 2 of the opposite state

Remember that rotations still match

Ring: (NULL, DATA, NULL, NULL, NULL) (2 states) – Only the first DATA can move, as it is the only stage followed by 2 of the opposite state
Ring: (NULL, DATA, DATA, NULL, NULL) (2 states) – Either state can move
- Ring: (NULL, DATA, DATA, DATA, NULL) (2 states) – Either state can still move
- Ring: (NULL, NULL, DATA, NULL, NULL) (2 states) – Only DATA can move

In the odd case, we can get up to (N+1)/2 states to fit. One thing to note is that when the pipeline is full (max number of states) only one state can move at a time in the odd case. In the even case, there’s that extra space that doesn’t get us another state, but it does give the states some wiggle room: more than one state can be advancing at a time.

From the above, we get: NumStages=NumStates+Advancement where Advancement is the maximum number of states that can advance at a time. Advancement must be greater than 0, if it equals 0, the pipeline will be locked. If Advancement>=NumStates then there’s no real advantage to adding more stages, unless the stages are not delay-matched.

Note: NumStates is always even in a ring.

Experiment

We’ll start with a full pipeline (Advancement=1) and then try a throughput-optimized design (Advancement=NumStates) where every state can advance simultaneously. By using the same number of states, we can benchmark the throughput and latency of the two.

Lest use NumStates:=4, which corresponds to 2 NULL and 2 DATA states.

Minimized Pipeline

By our formula above, we need 4+1=5 stages. The initial state:

By putting the value of 0 in the first DATA state, and 1 in the second state, we can track when the ring completes a cycle. Throughput is 2/t_complete (two DATA states per trip around the ring) and latency is t_complete.

5-stage-4-state — 5-stage ring with 2 DATA states and 2 NULL states

Throughput: 1/(400 ns) = 2.5 MHz
Latency: 800 ns

This experiment used the static_loop VHDL file, and a specific test script.

Throughput-Optimized Pipeline

This version has 4+4=8 stages to go through, but all the states can move at the same time. Throughput should increase, but latency may increase as well. I’m not going to show the diagram because of size problems, but it’s a lot like the above, just with more stages.

Throughput and latency are calculated from the simulation, just as before. For optimal throughput and startup latency, arrange the states in pairs – 2 DATA, then 2 NULL, then 2 DATA, … – this increases the number of Advancement options at the start to the maximum: NumStates.

8-stage-4-state — An 8-stage ring with 2 DATA states and 2 NULL states

Throughput: 1/(160 ns) = 6.25 MHz
Latency: 320 ns

This experiment used the static_loop VHDL file, and a specific test script.

Results

It looks like the throughput-optimized pipeline indeed has a higher throughput: By adding 3 states, we were able to more than double the efficiency of the ring, if you look at the simulation waveforms, in the first one only one stage is transitioning at a time. In the second, 4 stages are transitioning at a time. The second (faster) version uses 8/5 the resources though, so the decision on how many stages to use depends on available die space as well. In simulation, we don’t have to worry about this.

Commits: 997b4bb, be37b7f, 20ddd65

July 27, 2017

Register Ring

I want to start in on some sequential logic. We have a few combinational modules that we can build on already, so the est thing would be to make a sequential-only circuit. Once we’ve clarified how the concept works, we can add in combinational logic in.

By ‘sequential-only’, I am referring to a setup with only registers, it just passes it’s initial input in a loop forever, not changing it. I’m hoping it’ll help me with the concept a bit more, and flush out any issues with the registers.

Here’s a diagram of a three stage loop, just imagine the outputs loop back (drawing it would be messy):

Runtime Behavior

Let the initial state of the first stage’s outputs be DATA, with the first stage requesting NULL. The second and third stages are outputting NULL, and requesting DATA. Now let red be DATA, and blue be NULL.

After the gate delay for the register, the DATA wave is passed, and a request for NULL is sent back.

And, we’re back where we started

The ring will continue indefinitely. The VHDL source is available here, though without the test script, all stages remain at NULL, requesting DATA. I simulated this, and t turns out that it’s harder to see the pattern in graph form. To make things easier, I raised the number of stages.

At 8 stages, I start to be able to see it clearly as distinct wavefronts going through the pipeline. To make it really obvious, ramp it up to 12.

Not all stages shown.

And finally, if set at three, the pattern is harder to see, but it’s there. In the 3-stage case, the time spent requesting NULL and requesting DATA is the same for each stage.

If you use 2 stages, the system locks. A slideshow version of the ring pictures from above. As you can see, the transition to NULL only occurs while there are 2 DATA stages, and the transition to DATA only occurs while there are 2 NULL stages. This is so that no wavefront is ever ‘overwritten’. The second instance of that state saves the value.

July 24, 2017

Input Completeness

So, I have been doing more reading, and I found a concept that I think I glossed over up to this point. Input Completeness is the condition that the output should not change until all inputs are available. This must hold for both NULL->DATA and DATA->NULL wavefronts. I don’t actually understand why this is necessary yet.

I had vaguely considered the concept as weather or not internal lines would ever toggle more than once during a single data cycle, but I thought that since all data was expressed by asserted lines, a system couldn’t toggle as long as there were no inverters. Even if there was feedback, none of the gates use compliments of inputs, so adding more inputs either sets the gate, or leaves it alone. There is no way to clear a set line, without clearing an input. I will look into the reasons this condition is necessary at some point.

Quick thing: I will be using the term CSOP a bunch. It means Canonical Sum-of-Product. This is the version of the equation that has all of the truth table rows brought out separately. Even if the function can be optimized to eliminate a variable from a term or two, that would violate the rules of CSOP.

`The NULL->DATA Wavefront`

If the circuit is initially NULL (inputs, outputs, internals) then the outputs cannot change until all inputs are DATA. The simplest way to do this is to use the CSOP implementation. With CSOP, every input is used in one of the AND-Plane gates (either as DATA0 or DATA1). As such, none of the AND-Plane gates can trigger until all of the inputs have values.

The AND-Plane is the column of THNN gates that all the inputs tie into (all possible combinations of input DATA values).

`The DATA->NULL Wavefront`

The DATA->NULL transition for any individual gate is held until all its inputs go to NULL. As such, once an output is set, it won’t clear until its inputs clear. Unfortunately that only applies to the inputs involved in setting the output; in CSOP, again, this is all of them. If the output is not constructed with CSOP, then in some cases, some inputs won’t affect the outputs (think the unselected inputs of a MUX).

Solutions

It is not necessary to implement the function with CSOP, you can take the logic function and add (A.0+A.1) to the product terms that are missing A, for example. The function can then be simplified/expanded from there. This is described some here on page 17 (section 3.1):

Smith, Scott C., and Jia Di. Designing Asynchronous Circuits Using NULL Convention Logic (NCL) Scott C. Smith and Jia Di. San Rafael, Calif.]: Morgan & Claypool, 2009. Print. Synthesis Lectures on Digital Circuits and Systems #23.

I haven’t found a openly available source for this, if you are a student, check your university’s library website. If you do find a source, comment it.

July 13, 2017

NCL Register Design

We’ve covered some basics on NCL (signals and gates), next I’m looking into registers and structuring a system with multiple components.

Theory

In synchronous logic, designers use flip-flops to store data, they store the current value on every clock edge, moving it to the next stage. In asynchronous logic, there is no clock edge, so saving data requires something else. NCL uses threshold gates as registers, which works because of their hysteresis property. The requirements for the register:

Hold on to the value for as long as the next module needs it
Send a reset (NULL) signal to the next module on all inputs when it needs it
Let the previous register know what it needs (DATA/NULL)

So, there’s handshaking going on here, each register tells the one before it what it needs, and tries to send the next one what it asks for.

Design

How do we send the request to the previous module then? Lets assume 1 control line, and see if we need something else later. Since we are representing NULL with 0, lets set a request for null to be 0, and a request for data to be 1. We want to receive data as soon as the module has reset to NULL, and we want NULL as soon as the module is outputting data on all groups. Here’s the initial design:

NCL Register

If both A and B have a line set (either 0 or 1) then the ‘watcher’ gate is set. The little circle on the tip is an inverter, it turns the 1 (indicating we have DATA) to a 0 (indicating we want NULL) and vice versa.

There is one more requirement: If the module after us is requesting DATA, we can’t store the NULL wavefront (which would overwrite the DATA values) and vice versa and so need to hold the previous module until we can. This means that the request has to be based on the register’s outputs, not its inputs.

Refresher: A group of NCL lines are the set of lines representing a single entity, only one can be active at a time, but it is allowable to have none active (NULL).

NCL Register

Here we have a gate saving each bit: If the control input is low, then the gates will reset when the previous module’s outputs clear (next module requesting null). If the control input is high, then the gates will save DATA inputs (next module requesting DATA).

When both groups (A and B) have data, the watcher sees 2 data lines, sets its output, which goes through the inverter and requests NULL (which won’t be saved until the next module requests NULL).

Eventually, the previous module NULLs out and waits for a DATA request. When the next module requests NULL, the register gates flip to NULLs and the watcher outputs a 0, which is inverted to a 1 (request for DATA). The NULL wavefront passes through the module to the next register.

This cycle continues.

Notes

Components can be directly linked without registers, but only one operation can occur between registers at a time. Adding the registers splits up the operation into smaller parts, which can occur in parallel (for different inputs). At the start, the first set of inputs is loaded, and when they move to the second stage, the first is NULLed, after that, the first stage receives the second set of inputs, while the first set is still running through the third stage. this continues, with all data wavefronts separated by NULL wavefronts.

July 10, 2017

Handshaking & Pipelining

Generally speaking (in this context), handshaking is the process of electronic systems agreeing on what to do next. In NCL, this takes the form of modules requesting a NULL or DATA signal.

The request for NULL indicates that the operation has been performed, and the results saved for the next module to use.
The request for DATA indicates that the module has reset, passed the reset signal to the next module, and is ready for more work.

If you’re having trouble, think of it like two people doing laundry, one is operating the washing machine, the other is operating the dryer. Additionally, assume that the operators can’t be sure of how long a load will take in either stage. It’s not a perfect analogy, but it might help. Initially, both are empty:

In the empty state, the washing machine operator knows he or she needs clothes, so he or she finds some and puts them in the wash. The drier is also empty, but it needs to get its clothes from the washer, so it has to wait.
When the washer is finished, the operator takes out the clothes and pus them between the washer and dryer, for the dryer’s operator to use when ready. Since the washer is now ‘reset’, it is ready for clothes again, its operator loads it.
The dryer operator sees the clothes are ready to be dried and puts them in the dryer. Eventually they finish and leave the system.

Now, imagine that after a few loads, the dryer can’t keep up, and the washing machine finishes a load while the dryer is still running. The load goes into the space between the washer and dryer. Since the washer can’t know how close the dryer is to completion, it has to wait for the dryer to finish and take the waiting load before starting another.

July 10, 2017

Null Convention Logic Gates

See this post for information about NCL signals.

Symbol

It may or may not surprise you to know that NCL has it’s own set of gates for building circuits. They are called threshold gates and are drawn as

with the ‘threshold number’ in the middle. The inputs come in on the left (round) part, and the output comes out the point on the right.

Operation

For all threshold gates:

If all inputs are 0, the output is 0
If the number of inputs that are set is >= the threshold number, the output is 1
Otherwise, it holds its value.

threshold gates can have input weights, meaning that an input can count towards the threshold count more than once.

Notation

A threshold gate is denoted as THmn where m is the threshold value (the number of inputs needed to transition to a 1) and n is the total number of inputs. If weights are needed, then THmnW## is used, where the #’s are replaced with the weights (order is irrelevant). A TH23W2 gate sets when the first input is set (as it is counted twice), or when both of the other 2 are set. The boolean logic function is

TH23W2 Set: A+BC

Note that when just B or C are set, the gate keeps its value, so if it was a 1, then it will stay a 1, and if it was a 0 it will stay a 0. The logic function for clearing the gates is essentially the same for all:

THm1 Clear: A'
THm2 Clear: A'B'
THm3 Clear: A'B'C'
THm4 Clear: A'B'C'D

Summary

Threshold gates are used in NCL because they are less volatile than standard gates. Once they have an output, they hold on to int until their inputs are completely cleared (circuit reset). This means that a NCL component’s output will not flip more than once in an operation. This property of threshold gates means that if the outputs are set, the component has completed, and if they are reset, it has cleared. You always know when it is ready to move on.

July 9, 2017

Null Convention Logic Signals

If you don’t yet know what asynchronous logic is, I recommend reading this post (or using Google).

For the time being, I will be focusing my efforts on Null Convention Logic (NCL). NCL is technically a separate logic system from boolean logic. For now, I’ll stick to considering it in the context of a boolean system. What that means is that all signals in the design will still be boolean, they will just represent something a little different.

In NCL, each signal (boolean value) still has 2 meanings, but they are changed. A value of 0 means NO_DATA/NULL and a value of 1 means DATA. Different signals have different Data assigned. To represent a standard boolean variable, 2 lines are needed, the encoding:

FALSE (0): DATA0=1, DATA1=0
TRUE (1): DATA0=0, DATA1=1
Null/Unknown: DATA0=0, DATA1=0

The new state, NULL is used when the circuit hasn’t determined a value for the line yet. Detecting completion of the circuit is then as simple as seeing if one line in each group is set. When all the outputs are assigned a value, the values are saved, and the circuit resets to NULL outputs.

Note, it is entirely possible to have more than two lines in a group. Imagine If I made a circuit that took in an 8-bit color value and outputted if it was mostly one of {Red, Green, Blue}. Instead of having 2 boolean variables for 3 states (wasting a combination), I can have 1 three-state variable: {DATA_RED, DATA_BLUE, DATA_GREEN}. When the circuit is reset, the output is unknown, so all three go to NULL, when the inputs are received and the result found, the circuit sets one of the lines. This is not that different from ‘one-hot’ encoding in synchronous logic, except that it does have a defined all-off state that carries meaning (not data, but it does indicate circuit state). In synchronous logic, such a state would be an error.

The most common encodings I’ve come across so far are 2-rail {DATA0 and DATA1} and 4-rail {DATA0, DATA1, DATA2, DATA3}, representing 1 and 2 boolean variables respectively.

Anyways, that’s the basics of NCL signaling. The thing to remember is that the signals have to go to NULL between calculations, otherwise, there’s no way to know when they are ready.