Shifter

Theory

A Shifter takes an array of bits, and shifts them right of left. Numerically, this is like multiplying or dividing by 2 (in the case of binary numbers). Some examples:

Direction	Input	Shift Amount	Output
Right	`001001`	1	`000100`
Left	`001001`	1	`010010`
Right	`001001`	2	`000010`
Left	`001001`	3	`001000`

This could be applied to non-binary variables as well (like 3-rail signals) but the exact meaning will be different. There are a few ‘extensions’ to this behavior I’d like to add:

Rotation
Arithmetic shifting

Rotation allows the bits shifted out one end to be shifted back in the other:

Direction	Input	Output
Right	`1001`	`1100`
Left	`1001`	`0011`

Arithmetic shifting treats the shift as a mathematical operation and preserves the sign of the number. It is only valid for right shifts.

Direction	Input	Output
Right	`100`(-4)	`110`(-2)
Right	`110`(-2)	`111`(-1)

The sign of a number is represented by leading 1’s in the MSB, so an arithmetic right shift adds 1’s into the leftmost bits, if the number was negative. This is accomplished by shifting in the MSB.

Design

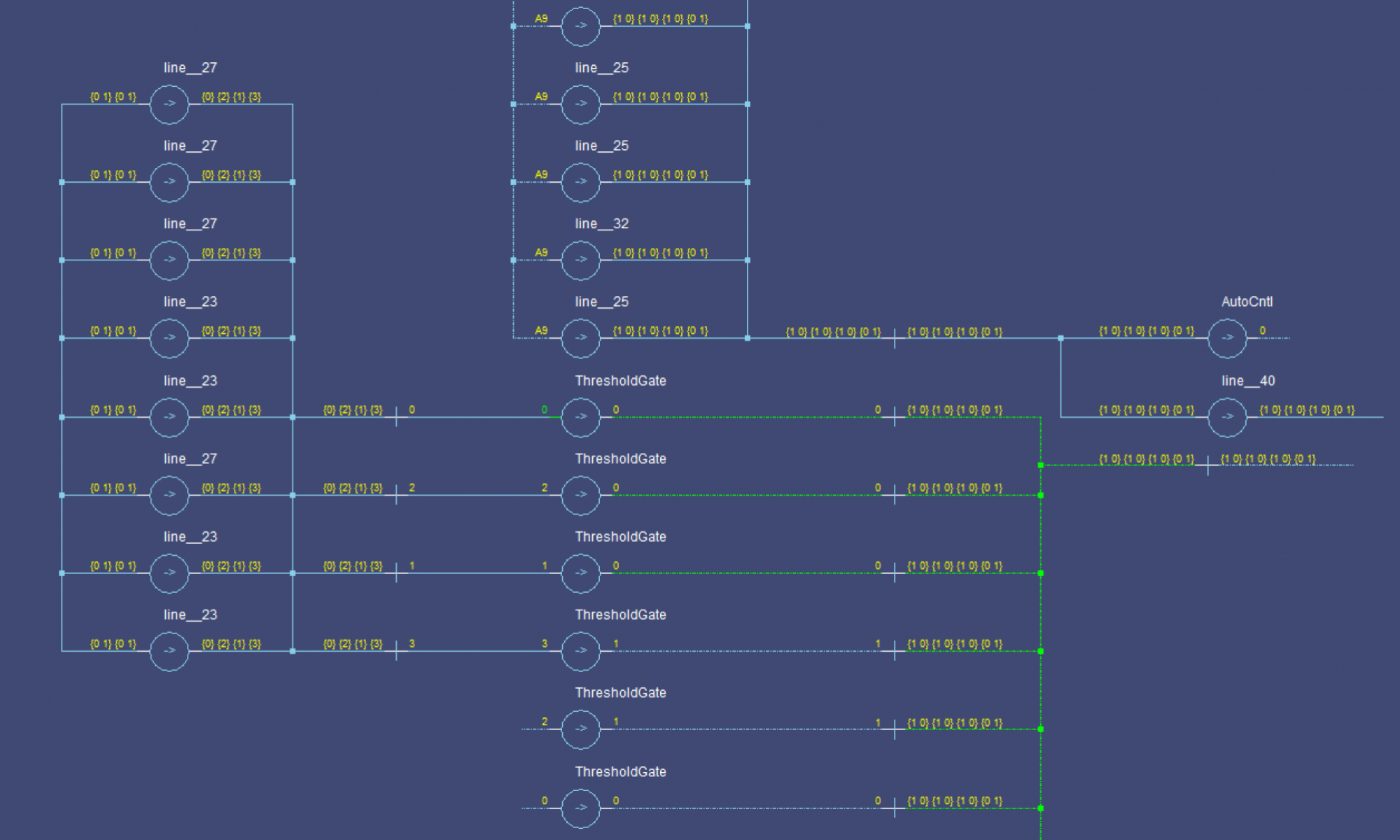
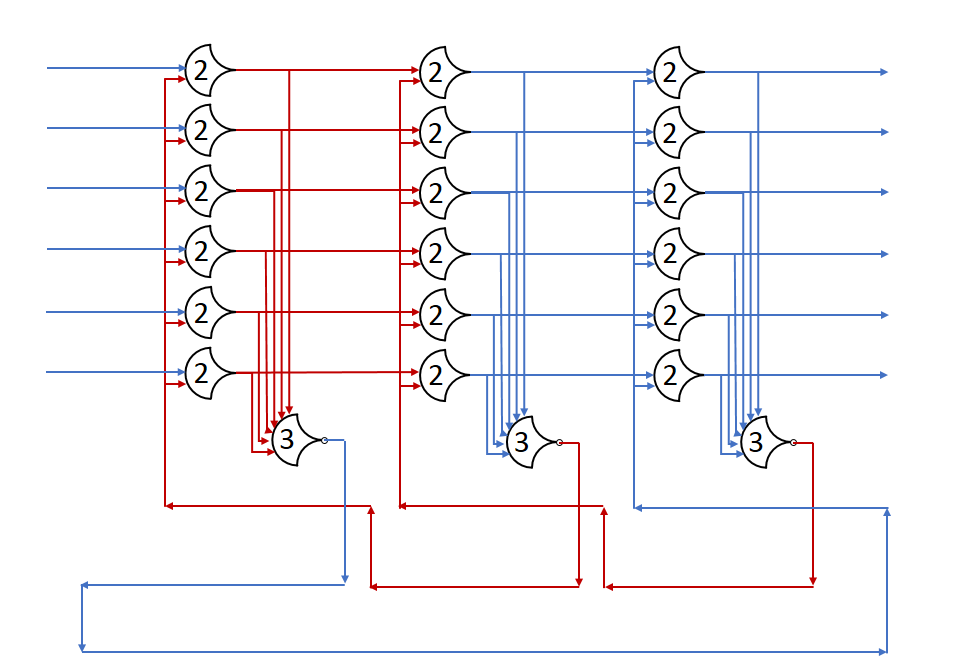
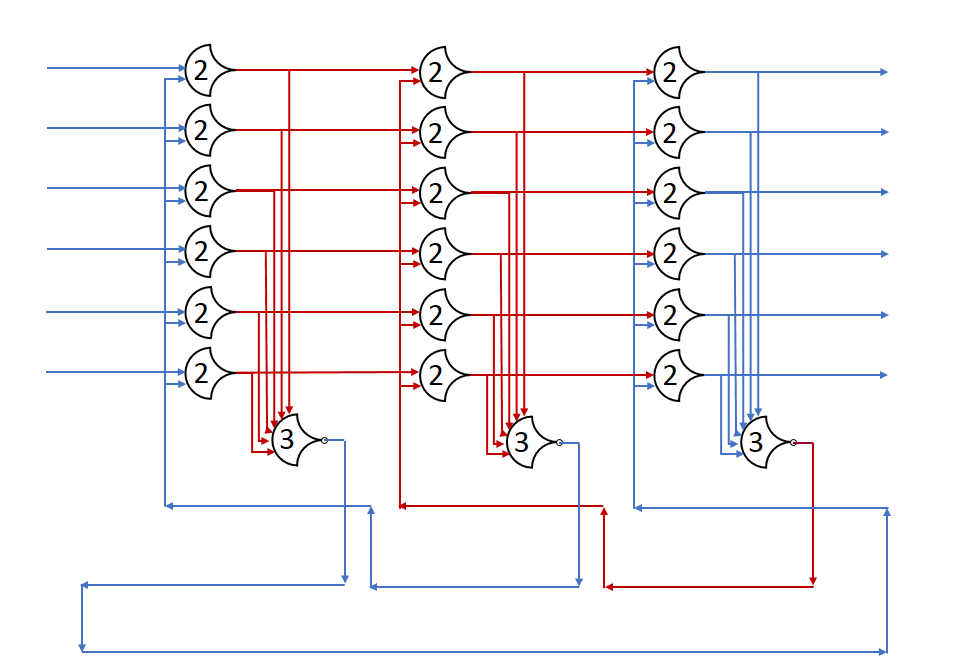
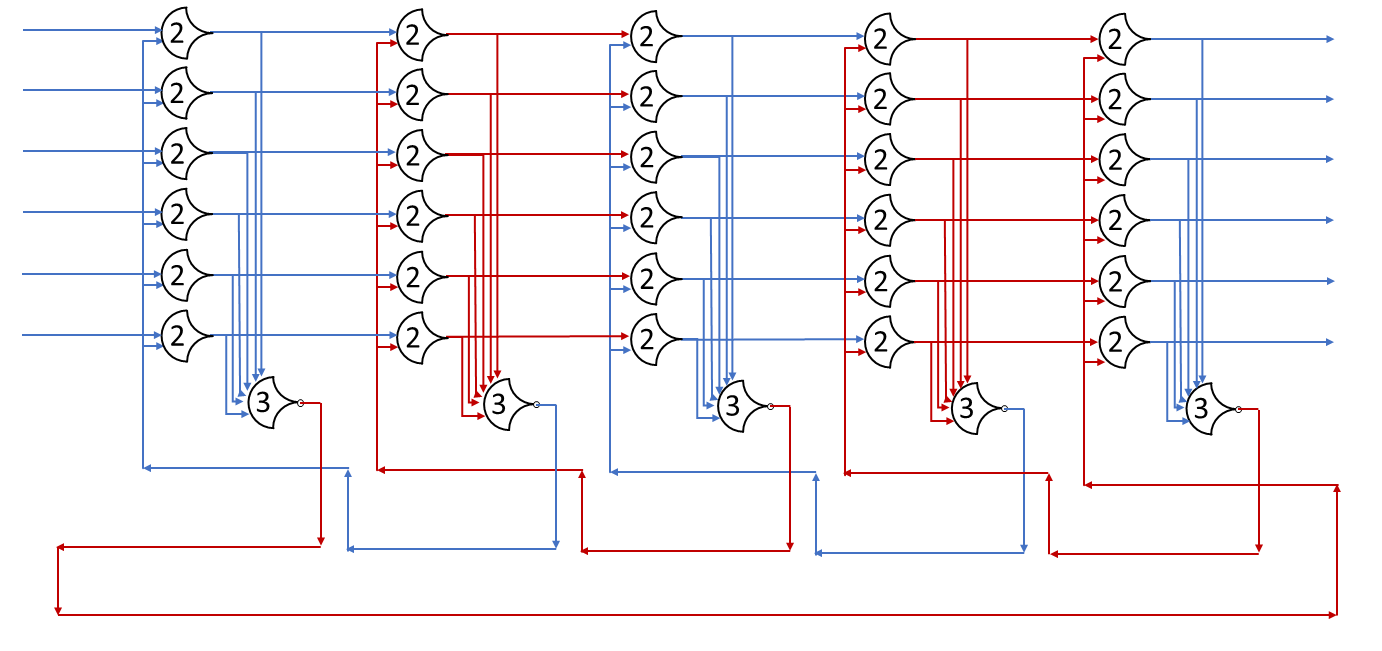
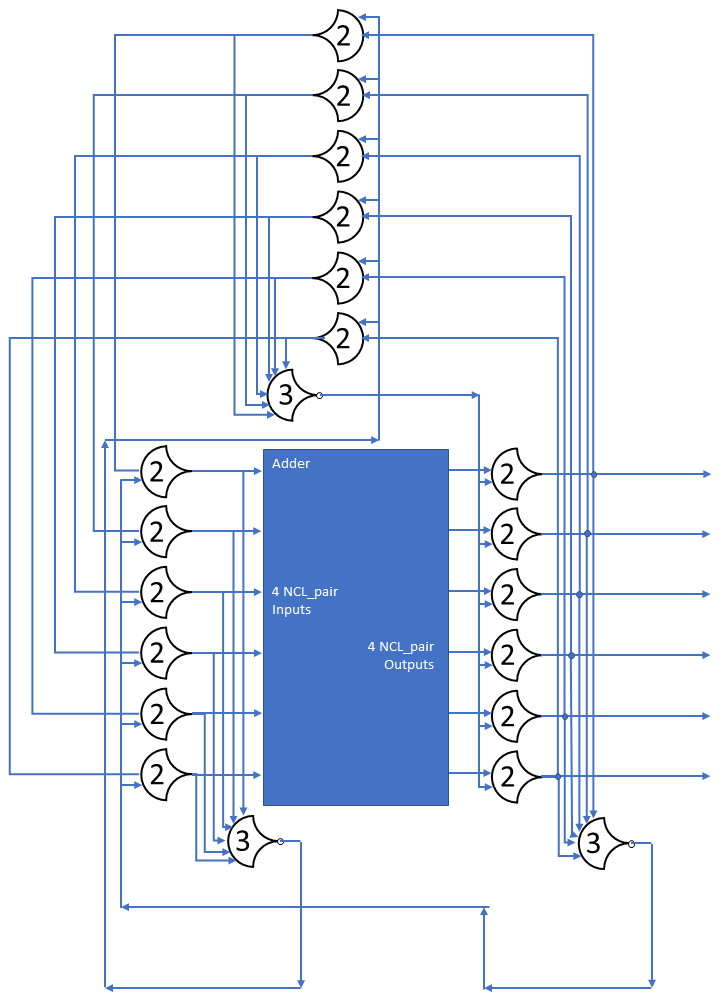
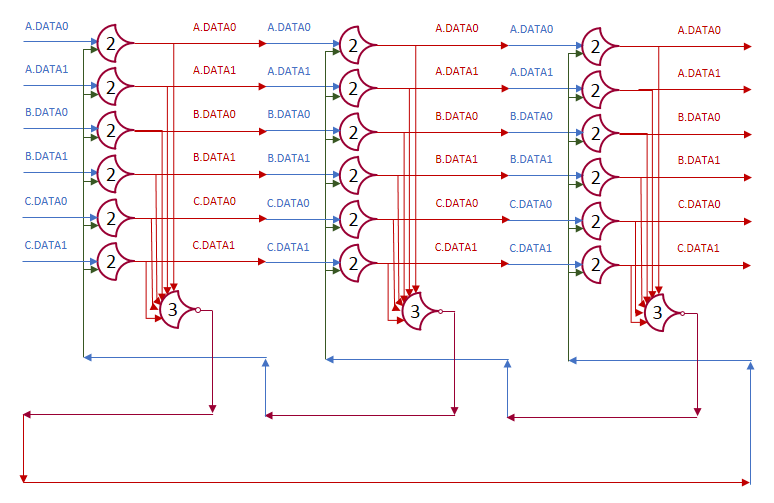
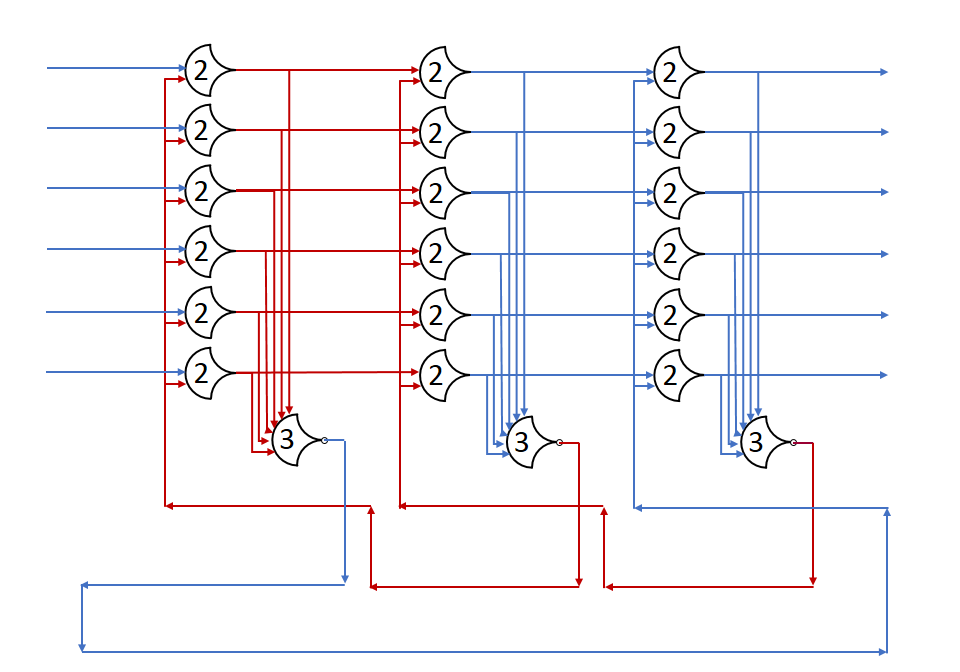
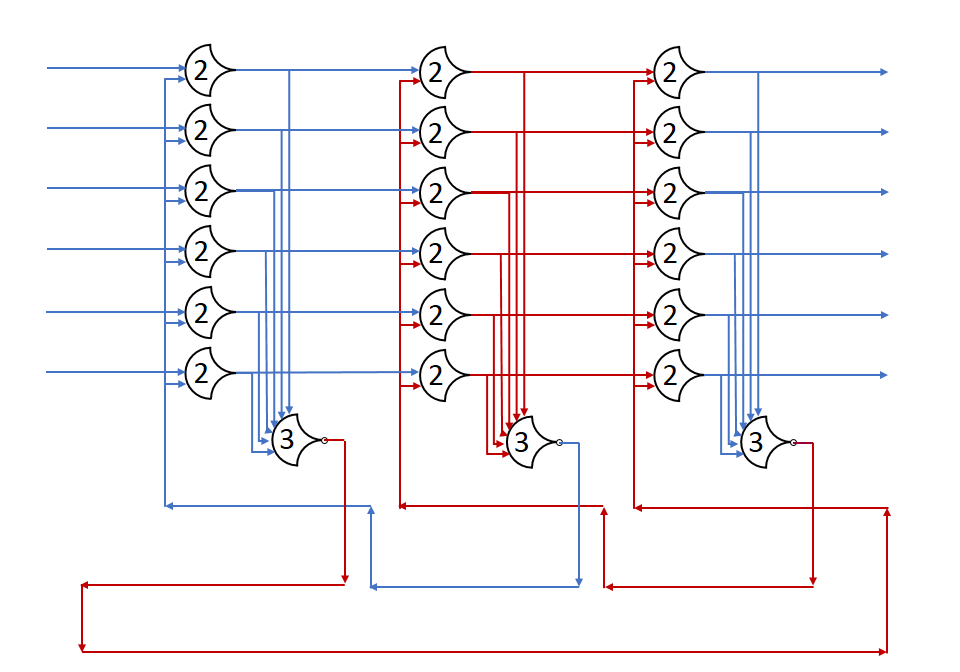
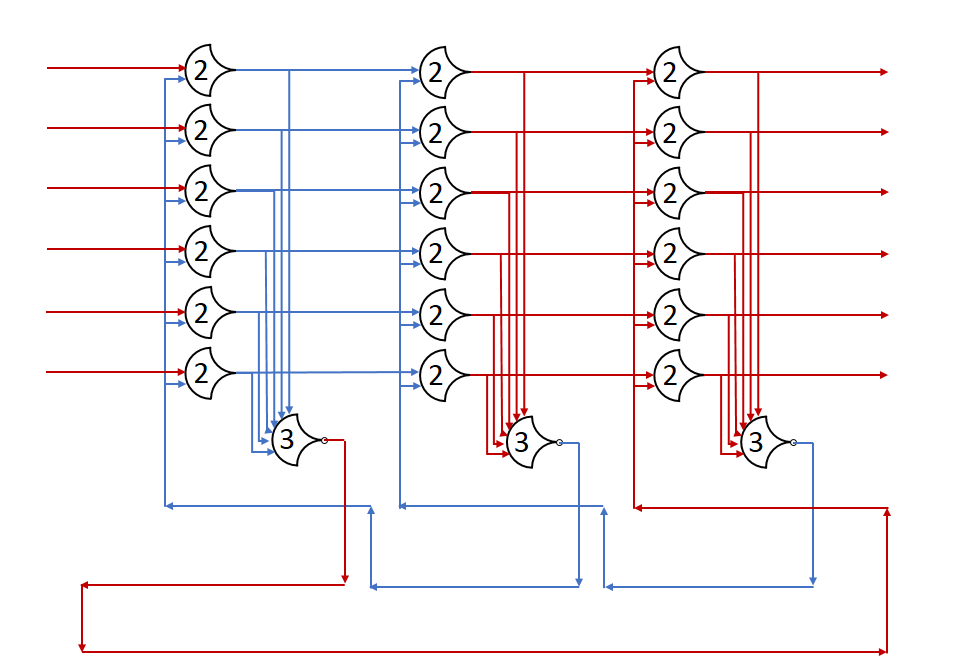
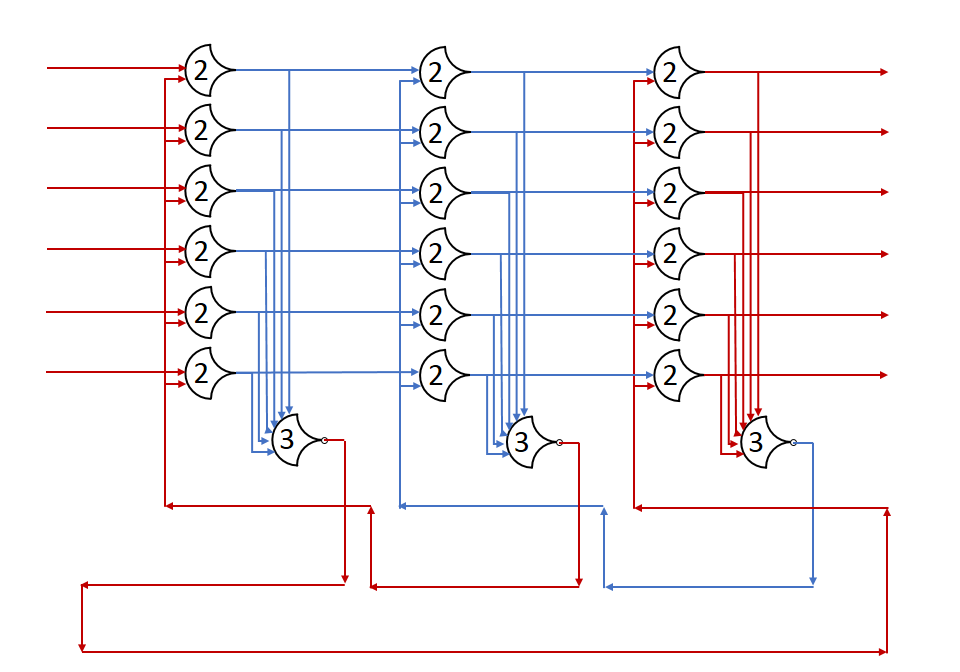
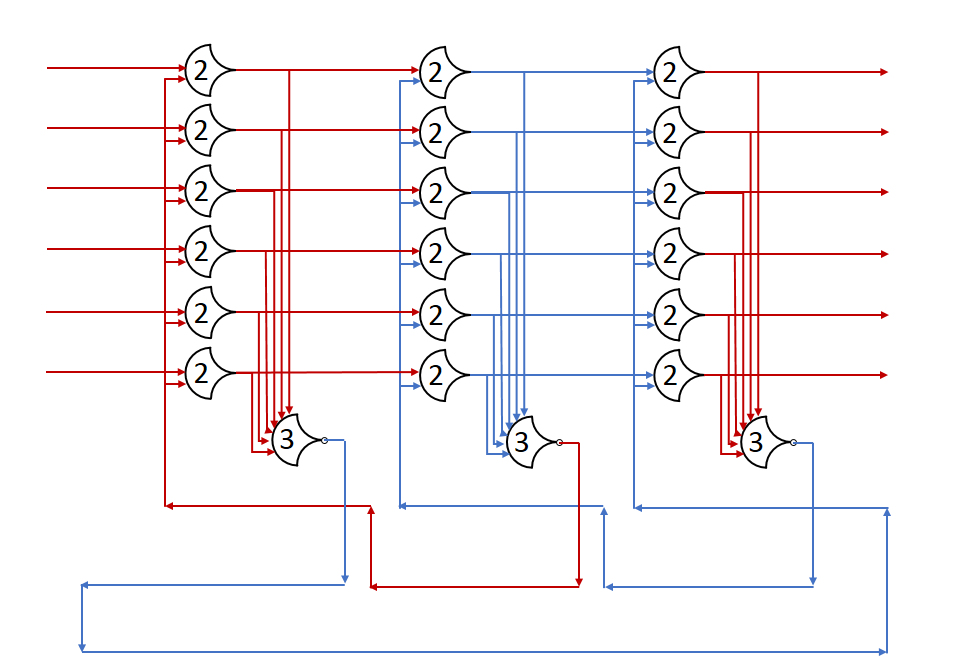
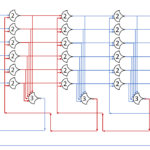
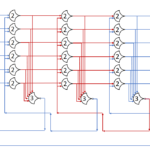
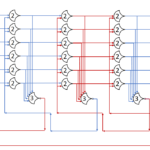
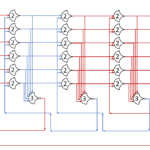
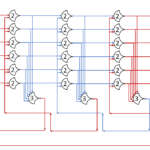
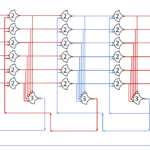
Each shift_amount bit corresponds to a shift of 2^n, where n is the index of the bit. Each constant-size shift can be accomplished with only wiring. As my CprE 381 professor always said, if you have two possible values, the easiest way to pick one is a MUX. So, each shift_amount bit will choose between an unshifted, or 2^n shifted value. By connecting these in layers, we get a shift of any size.

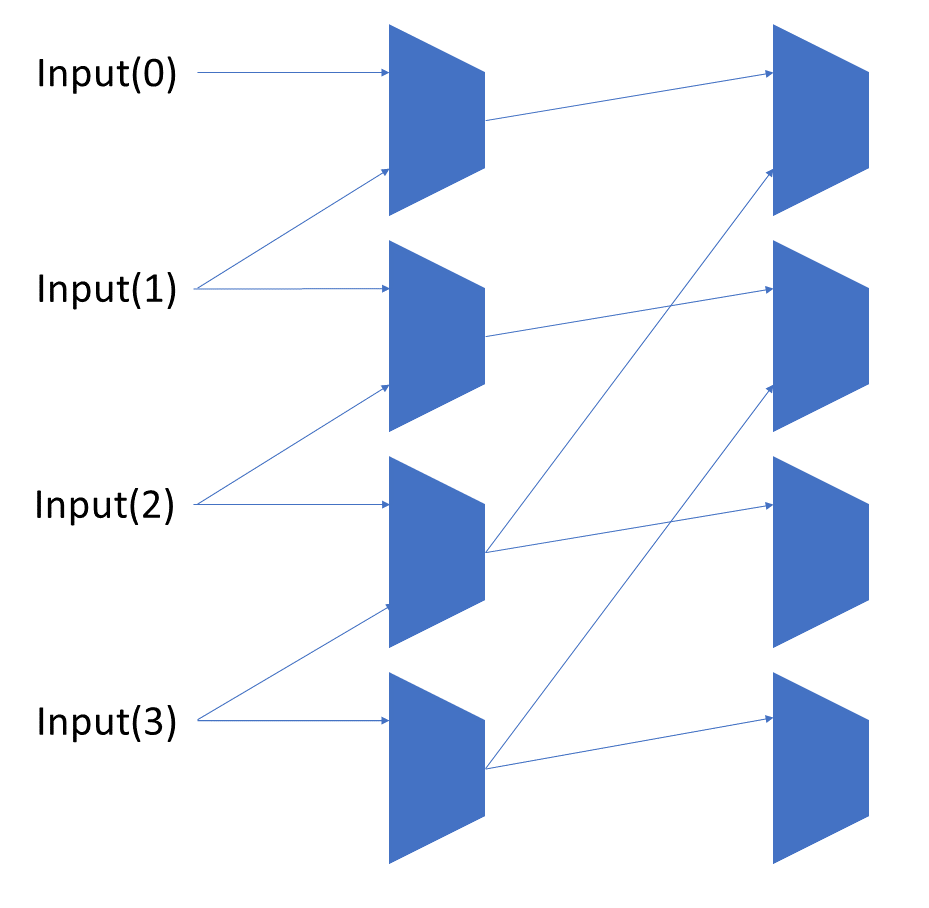
BasicShifter

The un-supplied inputs are 0’s. The first column is controlled by shift_amount(0), the second column is controlled by shift_amount(1).

To change the direction, we add a mux at the beginning that selects a reversed version of the input, let the shifter shift that, then un-reverse it at the end.

To add rotations, we add another input to the MUX’s at the bottom that feeds back from the top, so that the ‘lost’ bits are shifted back in.

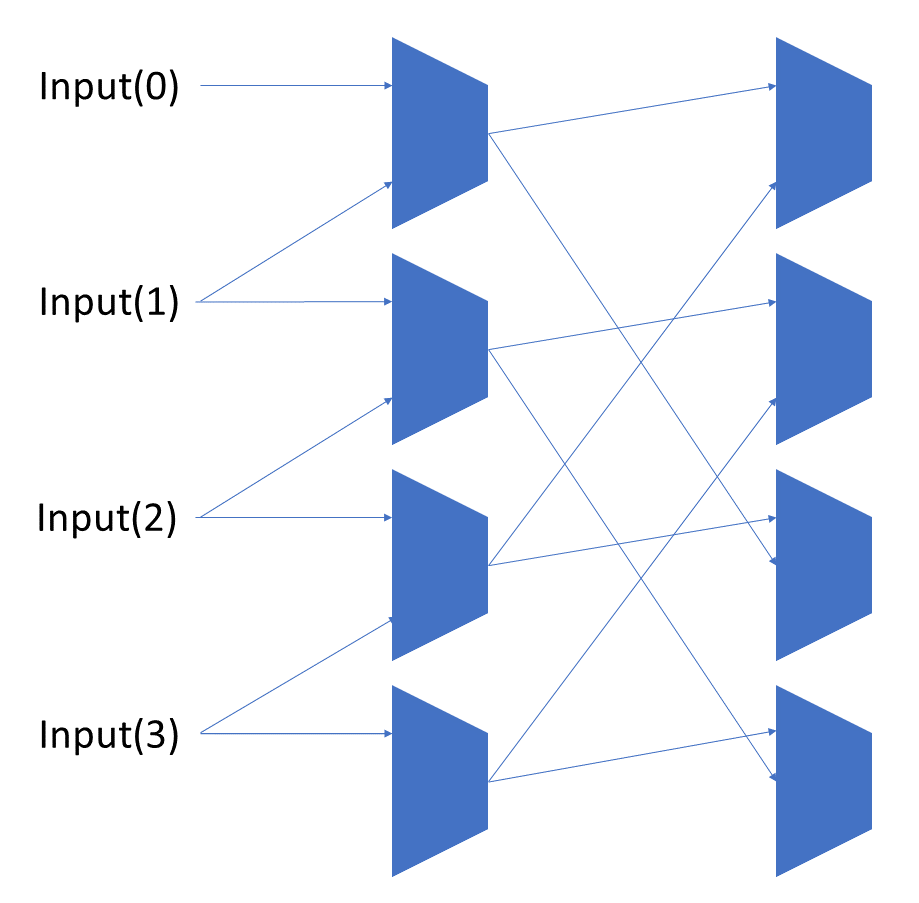
To add arithmetic operations, the unassigned inputs in the lower MUX’s are changed from 0 to the MSB of the input. This signal is constant across all the MUX’s it is applied to, so it is generated with a single MUX. On a left shift, the shifted-in value must be 0, so the MUX can only output the MSB when a right arithmetic shift is selected.

Implementation

the VHDL source, using generics to make it work for any number of inputs (even non-powers of 2, btw):

library ieee;
use work.ncl.all;
use ieee.std_logic_1164.all;

entity Shifter is
  generic(NumInputs : integer := 2);
  port(inputs       : in ncl_pair_vector(0 to NumInputs - 1);
       shift_amount : in ncl_pair_vector(0 to clog2(NumInputs) - 1);
       direction    : in ncl_pair;
       rotate       : in ncl_pair;
       logical      : in ncl_pair;
       output       : out ncl_pair_vector(0 to NumInputs - 1));
end Shifter;

architecture structural of Shifter is
  constant NumShiftAmountBits : integer := clog2(NumInputs);
  constant NumRows : integer := clog2(NumInputs);
  
  type RowSignals is array (integer range <>) of ncl_pair_vector(0 to NumInputs - 1);
  
  -- The shifted array at each stage of the shifter.
  signal rows : RowSignals(0 to NumRows);
  
  -- A generated value that is always DATA0 or NULL as appropriate
  signal zero_in : ncl_pair;
  
  -- The third input that is used for either logical or arithmetic operations.
  signal non_rotate_in : ncl_pair;

  signal input_reversed : ncl_pair_vector(0 to NumInputs - 1);
  signal output_reversed : ncl_pair_vector(0 to NumInputs - 1);

begin

  produceDATA0: THmn 
    generic map(M => 1, N => 2)
    port map(inputs(0) => inputs(0).DATA0,
             inputs(1) => inputs(0).DATA1,
             output => zero_in.DATA0);
  
  zero_in.DATA1 <= '0';   msb_in_mux: MUX     generic map(NumInputs => 4)
    port map(iOptions(0) => inputs(NumInputs-1),
             iOptions(1) => zero_in,
             iOptions(2) => zero_in,
             iOptions(3) => zero_in,
             iSel(0) => logical,
             iSel(1) => direction,
             output => non_rotate_in);

  in_bit_flipper: for i in 0 to NumInputs-1 generate
    input_reversed(i) <= inputs(NumInputs-1-i);     directionMux: MUX       generic map(NumInputs => 2)
      port map(iOptions(0) => inputs(i),
               iOptions(1) => input_reversed(i),
               iSel(0) => direction,
               output => rows(0)(i));
  end generate;

--  rows(0) <= inputs;

  rowsloop: for r in 0 to NumRows-1 generate
    columns: for c in 0 to NumInputs-1 generate
      ifstd: if (c + (2**r)) < NumInputs generate         multiplexer: MUX           generic map(NumInputs => 2)
          port map(iOptions(0) => rows(r)(c),
                   iOptions(1) => rows(r)(c + (2**r)),
                   iSel(0) => shift_amount(r),
                   output => rows(r+1)(c));

      end generate;

      ifwrp: if (c + (2**r)) >= NumInputs generate
        multiplexer: MUX
          generic map(NumInputs => 4)
          port map(iOptions(0) => rows(r)(c),
                   iOptions(1) => non_rotate_in,
                   iOptions(2) => rows(r)(c),
                   iOptions(3) => rows(r)((c+(2**r)) mod NumInputs),
                   iSel(0) => shift_amount(r),
                   iSel(1) => rotate,
                   output => rows(r+1)(c));

      end generate;
    end generate;
  end generate;

  out_bit_flipper: for i in 0 to NumInputs-1 generate
    output_reversed(i) <= rows(NumRows)(NumInputs - 1 - i);     outMux: MUX       generic map(NumInputs => 2)
      port map(iOptions(0) => rows(NumRows)(i),
               iOptions(1) => output_reversed(i),
               iSel(0) => direction,
               output => output(i));
  end generate;

end structural;

This code generates the necessary multiplexers for shifting the signal, flipping it at the input and output, and selecting how to handle the bits that can’t be shifted normally (because the source is out of range).

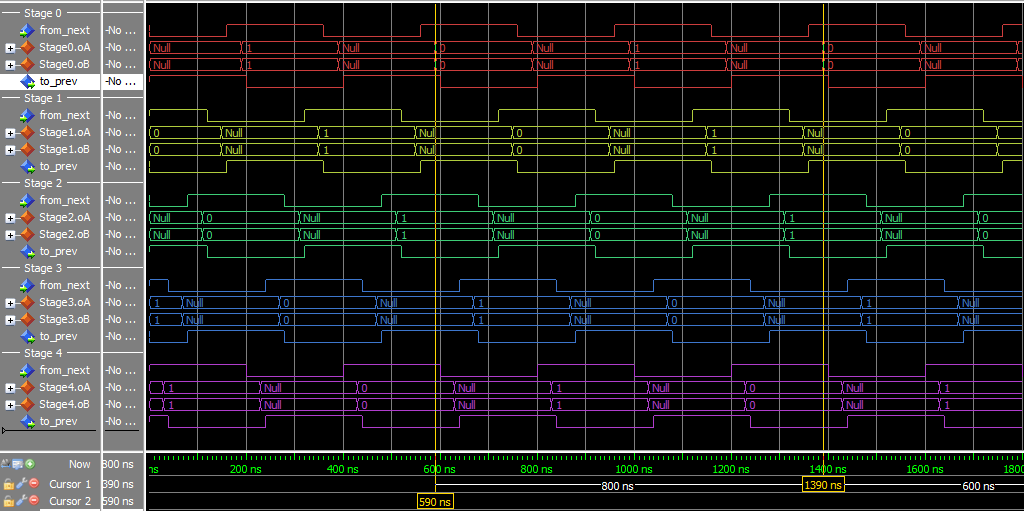
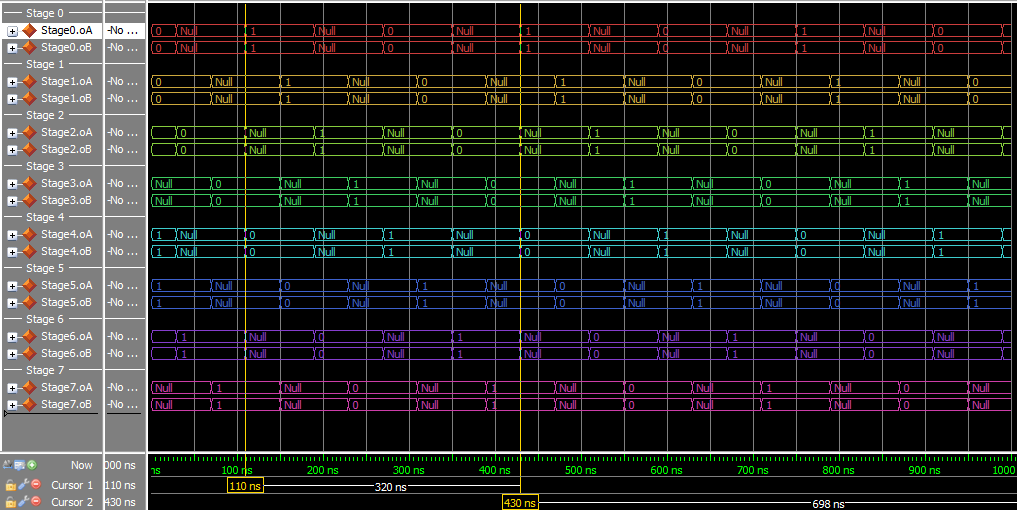
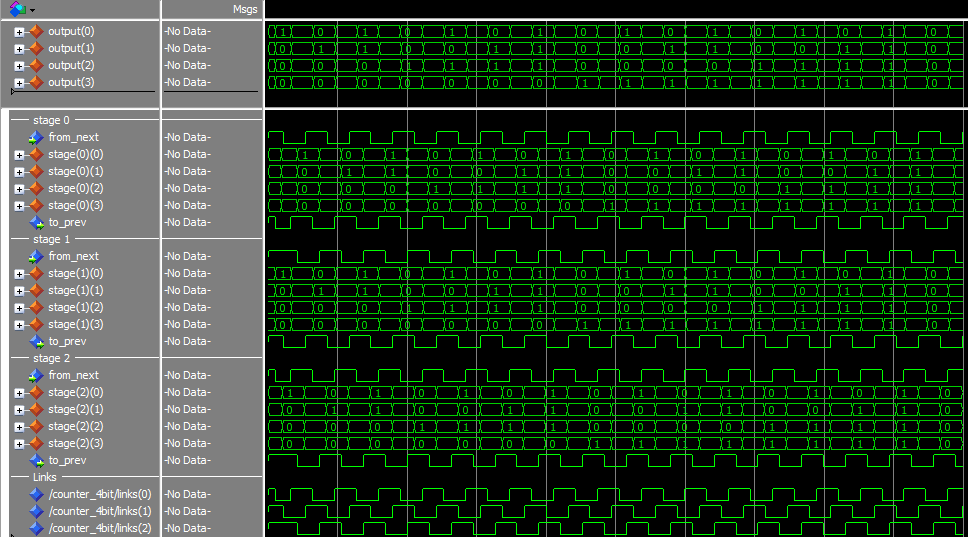
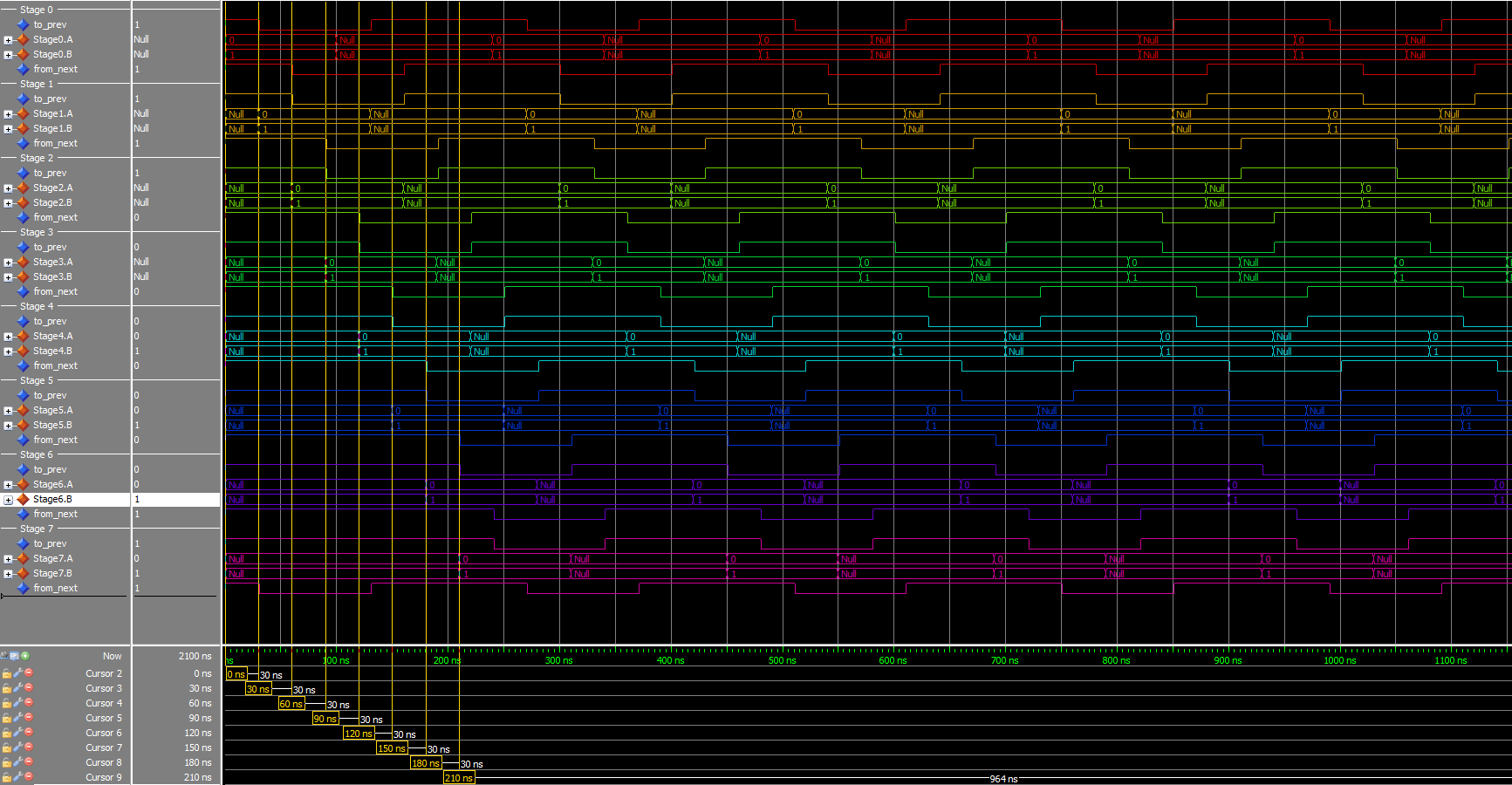
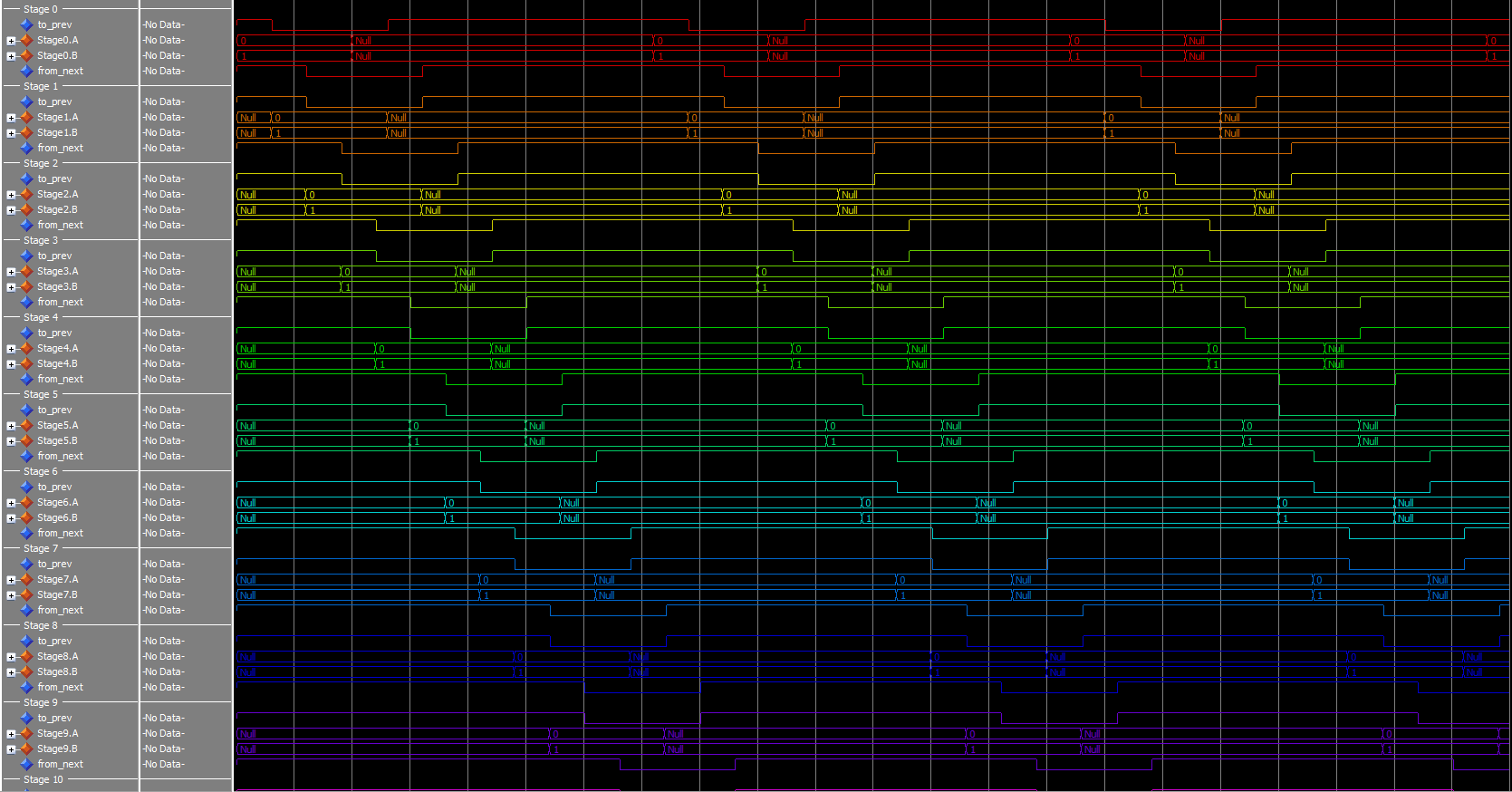
Testing

I made a simple test script to run through some cases. Everything seems to check out, here’s a sample:

Commit: 53d34cf, ef416eb

August 3, 2017

Null Convention Logic Signals II

Background

My naming conventions have probably been misleading. I have mostly treated NCL bits as three-state logic (NULL, DATA0, and DATA1) this is a valid way to work with the data, but it is limiting. The better way to think of it is as individual 2-state logic lines (NULL and DATA).

Internally to a component, using single-rail signals is very helpful. Not only are single-rail signals the inputs to all NCL gates, but they can be used as links between components as well. Single-rail signals cannot really be passed through registers because they have to be asserted for the DATA wave to read as complete. This would prevent the signal from conveying meaning, as it would always have the same value during computations.

My Theory

This section is unverified theory. Please share your thoughts below.

I will b using _ to refer to a non-asserted rail (null) and ^ to refer to an asserted rail (data).

Another benefit of this view is that you get more flexibility in state encodings. Standard encodings (that I’ve come across) use mutually exclusive data lines. So a 3-rail signal would have 3 possible states and a 4-rail signal would have 4 states. By thinking of the data more in terms of DATA and NULL, you get to design your own state encodings. For example, with a 4-rail encoding, you could use the following 6 states: {__^^, _^_^, _^^_, ^__^, ^_^_, ^^__}.

State Space Restrictions

A state space is the set of valid states. We will use it here a little more specifically to refer to the valid DATA states. Not all state spaces will actually work for NCL, The completion logic has to be able to correctly identify completed states. For example, if we try to use the following for a 3-rail signal, we have a problem: {__^, _^^, ^^^}. If the result is the last state (^^^) and the data on line 0 arrives first, the completion logic will see it as a complete __^ and pass on the wrong result.

For any state, it has to be able to partially arrive, without looking like another state. This is required for delay insensitivity. A simple way to make this happen is to use M-hot states. By that I mean that each state will have the same number of rails asserted as data (^), and all such states can be used. The number of states in such an assignment for a N-rail signal is M Choose N or C(M, N). This has its maximum value when M=N/2. It also has the benefit that any incomplete state has at most M-1 rails set, which will never match another state.

The logic proof-y version: ∀x,y∈S:(x&y!=x) and (x&y!=y) must hold (& is the bitwise AND operator) where S is the state space.

Using this N/2-hot encoding, the states/rail is

Rails	States	State Increase Factor
1	1
2	2	2
3	3	1.5
4	6	2
5	10	1.6667
6	20	2

Using this encoding, you get nearly twice as many states for each rail you add. Using mutually-exclusive rails (1-hot) you get 1 extra state per rail. Even if you break it up into 2-rail pairs and use combinations of those values, you only double your state space for every 2 rails you add. In the table above, s you increase the number of rails, the factor approaches 2 for the odd numbers of rails as well.

In special cases, you might want a more complex encoding, some examples of valid state spaces:

{___^, ^_^_, _^__}
{__^^, ^___, _^__}
{^^^_, ^^_^, ^_^^, _^^^}
{^^^_, ___^}
{__^^, _^_^, _^^_, ^__^, ^_^_, ^^__}

Takeaway

While you can increase the compatibility of your modules by using a standard state space, sometimes you can reduce the number of rails by using more dense encodings. Additionally, signals that exist only between registers (are not passed on) can actually be 1-rail signals, which is something I have a hard time remembering when integrating components. These 1-rail signals can act as enable signals: They can be used to prevent data from propagating, or to allow it to propagate (remember steering).

August 2, 2017

Steering

Problem

In Null Convention Logic, all computation is done with oscillating DATA/NULL cycles. The NULL cycles clear the whole circuit, the DATA cycles perform the computation. This requires 2 transition sets per computation (Previous DATA => NULL => Next DATA). Sometimes the DATA output from a component will not be used (think the unselected inputs of a MUX).

Solution

When using steering, the DATA wavefront is only passed to the necessary components. In the case of a MUX, the outputs of these components are then combined as needed with TH1n gates:

Steering

The TH22 gates in this example do not allow the DATA wavefront to apss into the components unless they are selected by the DMUX1. During any particular DATA wavefront, only one of these components will be active at a time; the other component will remain NULL. This saves transitions, and thus power. This method also works if only some, or no inputs are shared.

Details

The DMUX1 component is a decoder, that only outputs the DATA1 lines. Technically, I think it matches the NCL network criteria, if you consider the outputs to be single rail outputs, which have only one DATA value. The DMUX1 is used to enable only the selected component.

We will use steering when our ALU has more than just the Adder with glue logic. At some point we’ll have a multiplier, and a shifter, only one of these will operate at a time.

For more on steering, see Karl Fant’s site. His blog posts have lots of good theory too.

August 1, 2017

NCL Arithmetic Logic Unit – ADD/SUB

Theory

An arithmetic logic unit (ALU) is a component that performs operations on (usually) two or more sets of inputs, and outputs results. The operation performed is designated by an Operation signal.

Design

Our ALU will start simple, and we’ll add more operations over time. First, let’s build an add/sub unit. I already have an adder, which can be used to subtract by swapping some signals: In single-rail (standard) logic, to subtract instead of add, the second input to the adder is inverted and the carry bit is set – in NCL, we invert the input by swapping DATA0 and DATA1.

The swapper operates as the following equations

output.0 = input.0*swap.0 + input.1*swap.1
output.1 = input.1*swap.0 + input.0*swap.1

These can be implemented with THxor0 gates:

output.0 = THxor0(input.0, swap.0, input.1, swap.1)
output.1 = THxor0(input.1, swap.0, input.0, swap.1)

Our add/sub module will have these on every bit on input to the adder, with iC having the swap signal fed directly into it. Swap will be exposed in the component’s port as the add/subtract selector:

Add_Sub

Green is iA, blue is iB, and red is iC on the Adder. If Control is asserted (DATA1) iB will be inverted and the carry in will be asserted as well, resulting in subtraction.

This module actually fulfills the interface of an ALU by itself, it has data inputs, and a opcode. When we add more operations, we’ll wrap it all up in a ALU block and add a MUX.

Implementation

To implement this in VHDL, we need 1 Adder module and 2*N THxor0 gates:

use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
use work.ncl.all;

entity AddSub is
  generic(NumBits : integer := 4);
  port(iA        : in ncl_pair_vector(0 to NumBits-1);
       iB        : in ncl_pair_vector(0 to NumBits-1);
       Operation : in ncl_pair;

       oS       : out ncl_pair_vector(0 to NumBits-1);
       oC       : out ncl_pair);
end AddSub;

architecture structural of AddSub is

  -- iB into adder, potentially inverted from entity input
  signal adder_iB : ncl_pair_vector(0 to NumBits-1);

begin

  plainAdder: Adder
    generic map(NumAdderBits => NumBits)
    port map(iC => Operation,
             iA => iA,
             iB => adder_iB,
             oS => oS,
             oC => oC);

  bits: for iBit in 0 to NumBits-1 generate

    inverter0: THxor0 -- DATA0, Potentially inverted
      port map(A => iB(iBit).DATA0,
               B => Operation.DATA0,
               C => iB(iBit).DATA1,
               D => Operation.DATA1,
               output => adder_iB(iBit).DATA0);

    inverter1: THxor0 -- DATA1, Potentially inverted
      port map(A => iB(iBit).DATA0,
               B => Operation.DATA1,
               C => iB(iBit).DATA1,
               D => Operation.DATA0,
               output => adder_iB(iBit).DATA1);

  end generate;

end structural;

Testing

AddSub-2bit

The 2-bit case above is a little small, but it runs quickly. I have tested the module up to 6 bits. To change the number of bits, change the number at the top of the test script. The first several cases (interpreted to decimal):

0+0=0
0-0=0
0+1=1
0-1=-1
0+2=2
0-2=-2

This test script does check the sum output, but it does not verify the carry out.

Commit: 55d8c9f

July 31, 2017

Register Ring with Multiple Wavefronts

In this post, we built a ring of registers and set a data wavefront loose in it. We added many stages, and watched the single wavefront run through them. In this post, I’ll show what happens with multiple wavefronts.

Theory

First, we should establish how many registers we need for some number of wavefronts. From the Register Ring post, we know that in order for a state (DATA or NULL) to pass on, the next two stages must both be in the opposite state. This prevents the passage from overwriting the next stage’s state completely, as it has already passed on to the next stage.

Here, the DATA state (red) can move on to the next stage because the NULL state has been passed up to the 3rd stage. By overwriting the 2nd stage, no state is lost, because stage 2 has already finished with the NULL state.

Here, stage 2 cannot pass DATA on to stage 3 because that would remove the NULL state entirely. If there were 4 stages, and the 4th was NULL, then the 3rd stage could accept data, since the NULL state would be preserved.

As you can see, the number of stages in a state is not important, but rather the sequence must be preserved. Let’s assume a really long line of registers for a moment, with stage states: (DATA, NULL, NULL, DATA, ...) All of these NULLs can be assumed to be the same logical state, which we’ll refer to as NULL1, we’ll also call the first DATA state DATA1: (DATA1, NULL1, NULL1, DATA0, ...). Take the case where the last DATA wave can’t move because of some really slow stage after it. If we ‘run’ the system for a register delay, the DATA1 state progresses, and overwrites one of the NULL1 states, but there are still some left, so nothing is really lost. When DATA1 moves forward, a NULL state fills its stage; this is a new state, so let’s call it NULL2: (NULL2, DATA1, NULL1, DATA0, ...). If we run again, one might expect the DATA1 state to advance again, but taht would overwrite the NULL1 state completely, putting two distinct DATA states right next to each other. Having two adjacent DATA states prevents the components from resetting between them, which only produces correct results if the DATA states are identical. Since there is no guarantee that DATA1 and DATA0 are identical, we have to preserve the NULL between them.

There are states which would be deadlocked, however, as long as the initial conditions are valid (not deadlocked), the handshaking ensures that these states never occur as a propagation of the circuit.

Some examples:

Ring: (NULL, DATA, NULL, DATA) (4 states) – Nothing can pass, the system is deadlocked (we can’t actually get here naturally)
Ring: (NULL, DATA, NULL, NULL) (2 states) – Only the DATA state can pass, the NULLs are contiguous, so they can be considered to be identical states
Ring: (NULL, DATA, DATA, NULL) (2 states) – Both states can pass, the DATA can overwrite the NULL in position 4, and the NULL can overwrite the DATA in position 2
Ring: (NULL, DATA, DATA, DATA) (2 states) – Only NULL can pass, if DATA was able to pass, the NULL could be deleted from the system
Ring: (NULL, NULL, DATA, NULL) (2 states) – Only DATA can pass, if NULL was able to pass, the DATA could be deleted from the system
Rotations of these work out to the same thing since it’s a ring

Note that DATA and NULL are symmetric and the values in the DATA wave don’t matter. You can swap instances of ‘NULL’ and ‘DATA’ and get a valid result.

In short, with an even number of stages, you can only have N/2 states. What about odd numbers?

Ring: (NULL, DATA, NULL, NULL, DATA) (4 states) – Only the first DATA can move, as it is the only stage followed by 2 of the opposite state
Ring: (NULL, DATA, DATA, NULL, DATA) (4 states) – Only the first NULL can move, as it is the only stage followed by 2 of the opposite state

Remember that rotations still match

Ring: (NULL, DATA, NULL, NULL, NULL) (2 states) – Only the first DATA can move, as it is the only stage followed by 2 of the opposite state
Ring: (NULL, DATA, DATA, NULL, NULL) (2 states) – Either state can move
- Ring: (NULL, DATA, DATA, DATA, NULL) (2 states) – Either state can still move
- Ring: (NULL, NULL, DATA, NULL, NULL) (2 states) – Only DATA can move

In the odd case, we can get up to (N+1)/2 states to fit. One thing to note is that when the pipeline is full (max number of states) only one state can move at a time in the odd case. In the even case, there’s that extra space that doesn’t get us another state, but it does give the states some wiggle room: more than one state can be advancing at a time.

From the above, we get: NumStages=NumStates+Advancement where Advancement is the maximum number of states that can advance at a time. Advancement must be greater than 0, if it equals 0, the pipeline will be locked. If Advancement>=NumStates then there’s no real advantage to adding more stages, unless the stages are not delay-matched.

Note: NumStates is always even in a ring.

Experiment

We’ll start with a full pipeline (Advancement=1) and then try a throughput-optimized design (Advancement=NumStates) where every state can advance simultaneously. By using the same number of states, we can benchmark the throughput and latency of the two.

Lest use NumStates:=4, which corresponds to 2 NULL and 2 DATA states.

Minimized Pipeline

By our formula above, we need 4+1=5 stages. The initial state:

By putting the value of 0 in the first DATA state, and 1 in the second state, we can track when the ring completes a cycle. Throughput is 2/t_complete (two DATA states per trip around the ring) and latency is t_complete.

5-stage-4-state — 5-stage ring with 2 DATA states and 2 NULL states

Throughput: 1/(400 ns) = 2.5 MHz
Latency: 800 ns

This experiment used the static_loop VHDL file, and a specific test script.

Throughput-Optimized Pipeline

This version has 4+4=8 stages to go through, but all the states can move at the same time. Throughput should increase, but latency may increase as well. I’m not going to show the diagram because of size problems, but it’s a lot like the above, just with more stages.

Throughput and latency are calculated from the simulation, just as before. For optimal throughput and startup latency, arrange the states in pairs – 2 DATA, then 2 NULL, then 2 DATA, … – this increases the number of Advancement options at the start to the maximum: NumStates.

8-stage-4-state — An 8-stage ring with 2 DATA states and 2 NULL states

Throughput: 1/(160 ns) = 6.25 MHz
Latency: 320 ns

This experiment used the static_loop VHDL file, and a specific test script.

Results

It looks like the throughput-optimized pipeline indeed has a higher throughput: By adding 3 states, we were able to more than double the efficiency of the ring, if you look at the simulation waveforms, in the first one only one stage is transitioning at a time. In the second, 4 stages are transitioning at a time. The second (faster) version uses 8/5 the resources though, so the decision on how many stages to use depends on available die space as well. In simulation, we don’t have to worry about this.

Commits: 997b4bb, be37b7f, 20ddd65

July 28, 2017

4-Bit Counter

Now that we’ve covered making data flow in circles, let’s use that to make a closed-system 4-bit counter. The module will have 4 state bits and 5 outputs (sum & carry out). To do this we’ll need an adder. I have a ripple carry NCL adder here.

We are going to put the adder between two registers, with a third register going back to hold the state during the NULL wavefront.

The circuit shown is for a 3-bit adder, just to save space. The concept is the same, just add a bit to each register. Additionally, the adder has a static “0001” input for the B operand, which clears to NULL when the A input goes to NULL, this could be synthesized as the lines that get asserted being gated with TH22 gates with the watcher gate output (non-inverted) being the second input.

The source for this can be found here, and the simulation script here. Below is a simulation of the circuit. The first rows are the output, the next 3 sets are the registers.

The output cycles from 0 to 15, then resets to 0. During the reset cycle, the Adder’s Carry Out bit is set.

Conclusion

This is a pretty simple sequential circuit, but it demonstrates how to properly feed back the data. The third register is needed because the ‘business logic’ has to be able to go to NULL, without the whole thing losing state.

Commit: 5854b0c

VHDL source, Test Script

N-bit Ripple Carry Adder

July 27, 2017

Register Ring

I want to start in on some sequential logic. We have a few combinational modules that we can build on already, so the est thing would be to make a sequential-only circuit. Once we’ve clarified how the concept works, we can add in combinational logic in.

By ‘sequential-only’, I am referring to a setup with only registers, it just passes it’s initial input in a loop forever, not changing it. I’m hoping it’ll help me with the concept a bit more, and flush out any issues with the registers.

Here’s a diagram of a three stage loop, just imagine the outputs loop back (drawing it would be messy):

Runtime Behavior

Let the initial state of the first stage’s outputs be DATA, with the first stage requesting NULL. The second and third stages are outputting NULL, and requesting DATA. Now let red be DATA, and blue be NULL.

After the gate delay for the register, the DATA wave is passed, and a request for NULL is sent back.

And, we’re back where we started

The ring will continue indefinitely. The VHDL source is available here, though without the test script, all stages remain at NULL, requesting DATA. I simulated this, and t turns out that it’s harder to see the pattern in graph form. To make things easier, I raised the number of stages.

At 8 stages, I start to be able to see it clearly as distinct wavefronts going through the pipeline. To make it really obvious, ramp it up to 12.

Not all stages shown.

And finally, if set at three, the pattern is harder to see, but it’s there. In the 3-stage case, the time spent requesting NULL and requesting DATA is the same for each stage.

If you use 2 stages, the system locks. A slideshow version of the ring pictures from above. As you can see, the transition to NULL only occurs while there are 2 DATA stages, and the transition to DATA only occurs while there are 2 NULL stages. This is so that no wavefront is ever ‘overwritten’. The second instance of that state saves the value.

July 26, 2017

NCL Decoder Implementation

Design Recap

The circuit diagram of the decoder:

DMUX2

This decoder will be generic, and be implemented much like the MUX.

Implementation

Each row will be generated based on it’s index. For each input:

If it is set:
- Use DATA0 for the DATA0 of that case’s output
- Use DATA1 for the DATA1 of that case’s output
If it is clear:
- Use DATA1 for the DATA0 of that case’s output
- Use DATA0 for the DATA1 of that case’s output

The DATA0 output sets are combined with a THN1, and the DATA1 outputs are combined with a THNN:

Rows: for i in 0 to NumOutputs - 1 generate
  cntlBits: for iBit in 0 to NumInputs - 1 generate
    Cntl0Selection: if (to_signed(2**iBit, NumInputs+1) and to_signed(i, NumInputs+1)) = 0 generate
      Gate0Inputs(i)(iBit) <= inputs(iBit).DATA1;
      Gate1Inputs(i)(iBit) <= inputs(iBit).DATA0;
    end generate;

    Cntl1Selection: if (to_signed(2**iBit, NumInputs+1) and to_signed(i, NumInputs+1)) > 0 generate
      Gate0Inputs(i)(iBit) <= inputs(iBit).DATA0;
      Gate1Inputs(i)(iBit) <= inputs(iBit).DATA1;
    end generate;
  end generate;

  Gate0: THmn
    generic map(N => NumInputs, M => 1)
    port map(inputs => Gate0Inputs(i),
             output => outputs(i).DATA0);
  Gate1: THmn
    generic map(N => NumInputs, M => NumInputs)
    port map(inputs => Gate1Inputs(i),
             output => outputs(i).DATA1);
end generate;

This assigns input cases to the gates. If any non-selected values are asserted, then the DATA0 line of that case is asserted.

Adding the declarations around it:

library ieee;
use ieee.std_logic_1164.all;
use work.ncl.all;
use ieee.numeric_std.all;

entity Decoder is
  generic(NumInputs : integer := 2);
  port(inputs  : in  ncl_pair_vector(0 to NumInputs-1);
       outputs : out ncl_pair_vector(0 to (2**NumInputs)-1));
end entity Decoder;

architecture structural of Decoder is
  constant NumOutputs : integer := 2 ** NumInputs;

  type GateInputs is array (integer range <>) of std_logic_vector(0 to NumInputs - 1);
  signal Gate0Inputs : GateInputs(0 to NumOutputs-1);
  signal Gate1Inputs : GateInputs(0 to NumOutputs-1);
begin
  Rows: for i in 0 to NumOutputs - 1 generate
    cntlBits: for iBit in 0 to NumInputs - 1 generate
      Cntl0Selection: if (to_signed(2**iBit, NumInputs+1) and to_signed(i, NumInputs+1)) = 0 generate
        Gate0Inputs(i)(iBit) <= inputs(iBit).DATA1;
        Gate1Inputs(i)(iBit) <= inputs(iBit).DATA0;
      end generate;

      Cntl1Selection: if (to_signed(2**iBit, NumInputs+1) and to_signed(i, NumInputs+1)) > 0 generate
        Gate0Inputs(i)(iBit) <= inputs(iBit).DATA0;
        Gate1Inputs(i)(iBit) <= inputs(iBit).DATA1;
      end generate;
    end generate;

    Gate0: THmn
             generic map(N => NumInputs, M => 1)
             port map(inputs => Gate0Inputs(i),
                      output => outputs(i).DATA0);
    Gate1: THmn
             generic map(N => NumInputs, M => NumInputs)
             port map(inputs => Gate1Inputs(i),
                      output => outputs(i).DATA1);
  end generate;
end structural;

Testing

I tested it for 2 inputs, to make sure the generics build correctly. The outputs do not go through all combinations, since only one is allowed to be DATA1 at a time. Here’s the test script

Capture

Commit: a58ee22

July 25, 2017

NCL Decoder Design

Theory

The decoder is like a backwards multiplexer, it uses the selector bits to output a DATA 1 on a single output, and DATA 0 on the others. This can be used to enable one of many modules, or just to change encoding from binary to one-hot.

Design

If you remember how we made the MUX module, we had a loop that generated a set of selector lines (DATA0 or DATA1 from each selector input) for each case. We will re-use this, but we will generate a TRUE and FALSE signal for each case (DATA0 and DATA1 of the corresponding output). The TRUE gate for each case will be a THNN, and the FALSE gate will be a TH1N. Here is what a Decoder2 module would look like:

DMUX2

The inputs to the TH1N gates (FALSE) are the opposing rails to the THNN gate of the same case.

CaseTrue='All bits for this case set'
CaseFalse='Any other bit set'

Any NULL input produces some NULL output: The THNN gates (TRUE) can’t set because they will always be missing an input, and for any particular input (missing a bit) there are two possible outputs: one with the bit set and one with it clear; these FALSE outputs will remain off as they need the DATA0 and DATA1 respectively from the missing input.

The decoder is actually a fairly simple gate. It is possible to split the DMUX into two parts: DMUX1, and DMUX0. These components would output the DATA1 and DATA0 lines respectively. They are not valid as complete NCL components, but they are useful: You can make a MUX by using a DMUX1 and 2*NumOptions TH22 gates. This might be especially useful when making a MUX that takes in multi-bit options. A single DMUX1 would be used to generate the control signals, and each signal of each bit of each option would be gated with the TH22 gates.

July 24, 2017

Input Completeness

So, I have been doing more reading, and I found a concept that I think I glossed over up to this point. Input Completeness is the condition that the output should not change until all inputs are available. This must hold for both NULL->DATA and DATA->NULL wavefronts. I don’t actually understand why this is necessary yet.

I had vaguely considered the concept as weather or not internal lines would ever toggle more than once during a single data cycle, but I thought that since all data was expressed by asserted lines, a system couldn’t toggle as long as there were no inverters. Even if there was feedback, none of the gates use compliments of inputs, so adding more inputs either sets the gate, or leaves it alone. There is no way to clear a set line, without clearing an input. I will look into the reasons this condition is necessary at some point.

Quick thing: I will be using the term CSOP a bunch. It means Canonical Sum-of-Product. This is the version of the equation that has all of the truth table rows brought out separately. Even if the function can be optimized to eliminate a variable from a term or two, that would violate the rules of CSOP.

`The NULL->DATA Wavefront`

If the circuit is initially NULL (inputs, outputs, internals) then the outputs cannot change until all inputs are DATA. The simplest way to do this is to use the CSOP implementation. With CSOP, every input is used in one of the AND-Plane gates (either as DATA0 or DATA1). As such, none of the AND-Plane gates can trigger until all of the inputs have values.

The AND-Plane is the column of THNN gates that all the inputs tie into (all possible combinations of input DATA values).

`The DATA->NULL Wavefront`

The DATA->NULL transition for any individual gate is held until all its inputs go to NULL. As such, once an output is set, it won’t clear until its inputs clear. Unfortunately that only applies to the inputs involved in setting the output; in CSOP, again, this is all of them. If the output is not constructed with CSOP, then in some cases, some inputs won’t affect the outputs (think the unselected inputs of a MUX).

Solutions

It is not necessary to implement the function with CSOP, you can take the logic function and add (A.0+A.1) to the product terms that are missing A, for example. The function can then be simplified/expanded from there. This is described some here on page 17 (section 3.1):

Smith, Scott C., and Jia Di. Designing Asynchronous Circuits Using NULL Convention Logic (NCL) Scott C. Smith and Jia Di. San Rafael, Calif.]: Morgan & Claypool, 2009. Print. Synthesis Lectures on Digital Circuits and Systems #23.

I haven’t found a openly available source for this, if you are a student, check your university’s library website. If you do find a source, comment it.